练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，已知A、B为两定点，且||=2c,C为动点且满足||=2a(a＞c＞0,a、c为常数)，D为AC中点，P在边BC上且·=0.

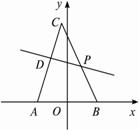
    （1）以AB所在直线为x轴，AB中点为坐标原点，建立如图所示的平面直角坐标系，求点P的轨迹方程.

    （2）若F、G是点P的轨迹上任意两个不同的点，且线段FG的中垂线与直线AB相交，交点为Q（t,0）.

    ①证明：存在最小的正数M，使得t＜M,并求M的值.

    ②若M=，求∠APC的取值范围.

    解：（1）∵,?

    ∴?

    根据椭圆定义可知P的轨迹方程为：?

    (其中b2=a2-c2,b＞0)?

    (2)①设G（x1 ,y1）,F(x 2 ,y 2),GF的中点（x 0 ,y 0）,斜率为k,?

    则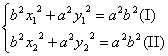

    (Ⅰ)-(Ⅱ)得b2x0+a2y0k=0.?

    若k=0,则FG的中垂线为y轴t=0；?

    若k≠0，则-=.?

    GF的中垂线方程为y-y0=(x-x0)，则-y0=(t-x0),t=-+x0-x0 .?

    ∵FG的中垂线与AB直线相交，?

    ∴-a＜x0＜a,∴-.?

    ∴存在最小正数M=,使得t＜M.?

    ②∵M=,∴,.?

    设∠APB=θ,||=r1 ,||=r2 ,?

    ∴r1+r2=2a,?

    ∴.

    ∴0°≤θ≤60°,∴∠APC∈(120°,180°］.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，已知E、F为平面上的两个定点|EF|=6，|FG|=10，且2
    EH
    =
    EG
    ，
    HP
    •
    GE
    =0    （G为动点，P是HP和GF的交点）．
    （Ⅰ）建立适当的平面直角坐标系求出点P的轨迹方程；
    （Ⅱ）若点P的轨迹上存在两个不同的点A、B，且线段AB的中垂线与直线EF相交于一点C，证明|OC|＜
    9
    5
    （O为EF的中点）．

    查看答案和解析>>

    科目：高中数学 来源：黄冈重点作业·高三数学（下） 题型：047

    如图，已知a、b是两条相互垂直的异面直线，其公垂线段AB的长为定值m，定长为n(n＞m)的线段PQ的两个端点分别在a、b上移动，M、N分别是AB、PQ的中点．

    (1)求证：AB⊥MN；

    (2)求证：MN的长是定值．

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：047

    如图，已知a、b是两条相互垂直的异面直线，其公垂线段AB的长为定值m，定长为n(n＞m)的线段PQ的两个端点分别在a、b上移动，M、N分别是AB、PQ的中点．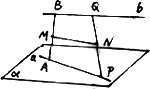

    (1)求证：AB⊥MN；

    (2)求证：MN的长是定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知A、B、C是直线m上的三点，且|AB|=|BC|=6，⊙O′切直线m于点A，又过B、C作⊙O′异于m的两切线，切点分别为D、E，设两切线交于点P，

    (1)求点P的轨迹方程;

    (2)经过点C的直线l与点P的轨迹交于M、N两点，且点C分所成比等于2∶3，求直线l的方程.

    查看答案和解析>>

    同步练习册答案