练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某种植基地将编号分别为1，2，3，4，5，6的六个不同品种的马铃薯种在如图所示的

    A

    B

    C

    D

    E

    F

    这六块实验田上进行对比试验，要求这六块实验田分别种植不同品种的马铃薯，若种植时要求编号1，3，5的三个品种的马铃薯中至少有两个相邻，且2号品种的马铃薯不能种植在A、F这两块实验田上，则不同的种植方法有 ( )

    A. 360种 B. 432种 C. 456种 D. 480种

    【答案】A

    【解析】由容斥原理，全排减去2站两端的，再减去，1,3，5不相邻，再加上2 站两端且1,3，5不相邻，所以N=360

    一类：恰两个相邻，选1,3,5中3个选两个排，再与另外4,6，排，最后插入2，不插两端，方法数=72，二类，三个相邻，1,3,5捆绑在一起，再与4,5排，最后插入2，不插两端，方法数360.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设a为实数，函数f（x）=（x﹣a）2+|x﹣a|﹣a（a﹣1）．
    （1）若f（0）≤1，求a的取值范围；
    （2）求f（x）在R上的单调区间（无需使用定义严格证明，但必须有一定的推理过程）；
    （3）当a＞2时，求函数g（x）=f（x）+|x|在R上的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|x+1|+|x|（x∈R）的最小值为a．
    （1）求a；
    （2）已知两个正数m，n满足m2+n2=a，求 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log3x．
    （1）求f（45）﹣f（5）的值；
    （2）若函数y=g（x）（x∈R）是奇函数，当x＞0时，g（x）=f（x），求函数 y=g（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为[5，15]，(15，25]，(25，35]，(35，45]，由此得到样本的重量频率分布直方图（如图）．

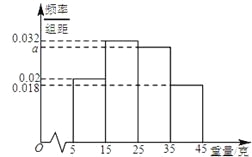
    （1）求的值；

    （2）从盒子中随机抽取3个小球，其中重量在[5,15]内的小球个数为X，求X的分布列和数学期望. (以直方图中的频率作为概率).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某影院为了宣传影片《战狼Ⅱ》，准备采用以下几种方式来扩大影响，吸引市民到影院观看影片，根据以往经验，预测：

    ①分发宣传单需要费用1.5万元，可吸引30%的市民，增加收入4万元；

    ②网络上宣传，需要费用8千元，可吸引20%的市民，增加收入3万元；

    ③制作小视频上传微信群，需要费用2.5万元，可吸引35%的市民，增加收入5.5万元；

    ④与商场合作需要费用1万元，购物满800元者可免费观看影片（商场购票），可吸收15%的市民，增加收入2.5万元，

    问: (1)在三个观看影片的市民中，至少有一个是通过微信群宣传方式吸引来的概率是多少？

    (2)影院预计可增加盈利是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣alnx+ ．
    （1）若a=1，求f（x）在x∈[1，3]的最值；
    （2）求函数f（x）的单调区间；
    （3）若存在x0∈[1，e]，使得f（x0）＜0成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】记等差数列的前项和为.

    （1）求证：数列是等差数列；

    （2）若 ，对任意，均有是公差为的等差数列，求使为整数的正整数的取值集合；

    （3）记，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱柱ABCD﹣A1B1C1D1的三视图如图所示，则异面直线D1C与AC1所成的角为（ ）
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    同步练习册答案