
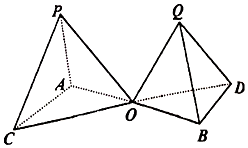
 如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短.
如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短. 分析 过点P作底面OAC的垂线交底面OAC于点O1,过点Q作底面OBD的垂线交底面OBD于点O2,连结O1O2,则四边形PO1O2Q是直角梯形,由此能求出当a=$\sqrt{m}$时,塔尖P,Q之间的距离最短.
解答 解:如图,过点P作底面OAC的垂线交底面OAC于点O1,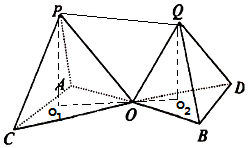
过点Q作底面OBD的垂线交底面OBD于点O2,
连结O1O2,则O1,O2,O三点共线,且PO1∥QO2,
则四边形PO1O2Q是直角梯形,
在Rt△OPO1中,OP=a,OO1=$\frac{2}{3}×\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{3}}{3}a$,则PO1=$\frac{\sqrt{6}}{3}a$,
同理,得OO2=$\frac{\sqrt{3}}{3}\frac{m}{a}$,QO2=$\frac{\sqrt{6}}{3}\frac{m}{a}$,
则PQ=$\sqrt{({O}_{1}{{O}_{2}}^{2}+(Q{O}_{2}-P{O}_{1})^{2}}$
=$\sqrt{(\frac{\sqrt{3}}{3}a+\frac{\sqrt{3}}{3}\frac{m}{a})^{2}+(\frac{\sqrt{6}}{3}\frac{m}{a}-\frac{\sqrt{6}}{3}a)^{2}}$
=$\sqrt{{a}^{2}+\frac{{m}^{2}}{{a}^{2}}-\frac{2}{3}m}$,
PQ=$\sqrt{{a}^{2}+\frac{{m}^{2}}{{a}^{2}}-\frac{2}{3}m}$≥$\sqrt{2\sqrt{{a}^{2}•\frac{{m}^{2}}{{a}^{2}}}-\frac{2}{3}m}$=$\frac{2\sqrt{3}}{3}$$\sqrt{m}$(${a}^{2}=\frac{{m}^{2}}{{a}^{2}}$,当a=$\sqrt{m}$时,等号成立),
则当a=$\sqrt{m}$时,塔尖P,Q之间的距离最短.
点评 本题考查两点间距离最小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
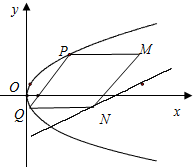 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={log_2}(\sqrt{{x^2}+1}-x)$ | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=x2-x3 | D. | f(x)=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 2 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正三棱柱ABC-A1B1C1中,AB=2,AAl=3,点D为C1B的中点,点P为AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AAl=3,点D为C1B的中点,点P为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com