
【题目】随着夏季的到来,冰枕成为市面上的一种热销产品,某厂家为了调查冰枕在当地大学的销售情况,作出调研,并将所得数据统计如下表所示:
表一:
温度在30℃以下 | 温度在30℃以上 | 总计 | |
女生 | 10 | 30 | 40 |
男生 | 40 | 20 | 60 |
总计 | 50 | 50 | 100 |
随后在该大学一个小卖部调查了冰枕的出售情况,并将某月的日销售件数(x)与销售天数(y)统计如下表所示:
表二:
第 | 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据表二中的数据在下列网格纸中绘制散点图;
(2)请根据表二中提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)从(1)(2)中的数据及回归方程我们可以得到,销售件数随着销售天数的增长而增长,但无法判断男、女生对冰枕的选择是否与温度有关,请结合表一中的数据,并自己设计方案来判段是否有99.9%的可能性说明购买冰枕的性别与温度相关.
参考数据及公式:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
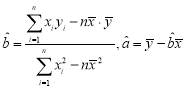 ;
;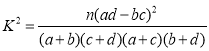 ,其中
,其中![]() .
.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,在向上平移一个单位,得到g(x)的图象.若g(x1)g(x2)=4,且x1,x2∈[﹣2π,2π],则x1﹣2x2的最大值为( )
个单位,在向上平移一个单位,得到g(x)的图象.若g(x1)g(x2)=4,且x1,x2∈[﹣2π,2π],则x1﹣2x2的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,记
,记![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)① 计算![]() ,
,![]() 的值;
的值;
② 猜想![]() ,
,![]() 满足的关系式,并用数学归纳法加以证明;
满足的关系式,并用数学归纳法加以证明;
(2)若数列![]() 通项公式为
通项公式为![]() ,证明:
,证明:![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
, ,
,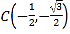 为圆上三个定点,某同学从
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
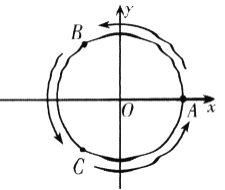
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系x![]() y中,曲线C的参数方程为
y中,曲线C的参数方程为![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线C的极坐标方程;
(2)设直线![]() 与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com