
已知a,b,c均为正数,证明:a2+b2+c2+ 2≥6
2≥6 ,并确定a,b,c为何值时,等号成立.
,并确定a,b,c为何值时,等号成立.
见解析
【解析】法一:因为a、b、c均为正数,由平均值不等式得
a2+b2+c2≥3(abc)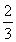 ,①
,①
 ≥3(abc)-
≥3(abc)- ,②
,②
所以 2≥9(abc)-
2≥9(abc)- .
.
故a2+b2+c2+ 2≥3(abc)
2≥3(abc) +9(abc)-
+9(abc)- .
.
又3(abc) +9(abc)-
+9(abc)- ≥2
≥2 =6
=6  ,③
,③
所以原不等式成立.
当且仅当a=b=c时,①式和②式等号成立.
当且仅当3(abc) =9(abc)-
=9(abc)- 时,③式等号成立.
时,③式等号成立.
即当且仅当a=b=c=3 时,原式等号成立.
时,原式等号成立.
法二:因为a,b,c均为正数,由基本不等式得
a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac,
所以a2+b2+c2≥ab+bc+ac.①
同理 ≥
≥ ,②
,②
故a2+b2+c2+ 2≥ab+bc+ac+3
2≥ab+bc+ac+3 +3
+3 +3
+3 ≥6
≥6 .③
.③
所以原不等式成立,
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,(ab)2=(bc)2=(ac)2=3时,③式等号成立.
即当且仅当a=b=c=3 时,原式等号成立.
时,原式等号成立.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用22练习卷(解析版) 题型:解答题
如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
已知矩阵M= .
.
(1)求矩阵M的逆矩阵;
(2)求矩阵M的特征值及特征向量.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C?PB?A的余弦值..
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
在极坐标系中,已知圆ρ=2cos θ与直线3ρcos θ+4ρsin θ+a=0相切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:解答题
如图,点P(0,-1)是椭圆C1: =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.

(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
已知椭圆 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:填空题
直线 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练3练习卷(解析版) 题型:选择题
已知点M(-3,0)、N(3,0)、B(1,0),动圆C与直线MN切于点B,分别过点M、N且与圆C相切的两条直线相交于点P,则点P的轨迹方程为( )
A.x2-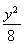 =1 (x>1) B.x2-
=1 (x>1) B.x2- =1(x>0)
=1(x>0)
C.x2-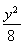 =1(x>0) D.x2-
=1(x>0) D.x2- =1(x>1)
=1(x>1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com