

 (单位:百件),每件利润
(单位:百件),每件利润 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)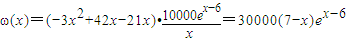 (5分)
(5分)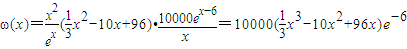


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
| x |
| 2 |
|
| 100ex-6 |
| x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省五市十高三第一次合检测理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
某商场根据调查,估计家电商品从年初(1月)开始的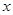 个月内累计的需求量
个月内累计的需求量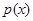 (百件)为
(百件)为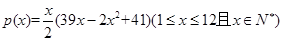
(1)求第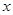 个月的需求量
个月的需求量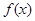 的表达式.
的表达式.
(2)若第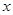 个月的销售量满足
个月的销售量满足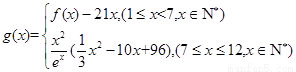 (单位:百件),每件利润
(单位:百件),每件利润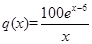 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 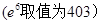
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
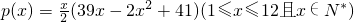
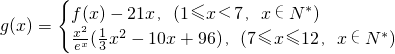 (单位:百件),每件利润
(单位:百件),每件利润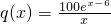 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?(e6取值为403)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com