
【题目】已知f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0
(1)求函数f(x)的解析式;
(2)若a>0,解关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).
【答案】
(1)解:(1)∵f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0,
∴ ![]() ,解得b=3,k=﹣1.
,解得b=3,k=﹣1.
∴f(x)=﹣x+3.
(2)解:∵a>0,x2﹣(a2+a+1)x+a3+3<f(x),
∴﹣x+3>x2﹣(a2+a+1)x+a3+3,
∴x2﹣(a2+a)x+a3<0,
解方程x2﹣(a2+a)x+a3=0,得x1=a, ![]() ,
,
当0<a<1时,原不等式的解集为:{x|a2<x<a};
当a=1时,原不等式的解集为:{x|x≠1};
当a>1时,原不等式的解集为:{x|a<x<a2}
【解析】(1)由已知得 ![]() ,由此能求出f(x).(2)原不等式等价于x2﹣(a2+a)x+a3<0,由此能求出关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).
,由此能求出f(x).(2)原不等式等价于x2﹣(a2+a)x+a3<0,由此能求出关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).


科目:高中数学 来源: 题型:
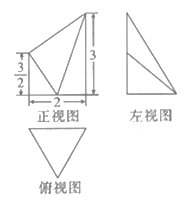
【题目】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
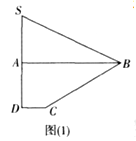
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
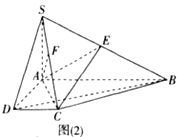
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.
(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表:
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | ﹣2 |
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的二面角的正弦值及四棱锥
所成的二面角的正弦值及四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com