
已知椭圆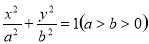 的离心率为
的离心率为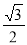 ,点
,点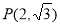 在椭圆上.
在椭圆上.
(1)求椭圆C的方程;
(2)设椭圆的左右顶点分别是A、B,过点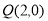 的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
(1)椭圆C方程是 ;(2)G的横坐标的值为8.
;(2)G的横坐标的值为8.
【解析】
试题分析:(1)由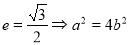 ,又点
,又点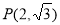 在椭圆上,所以
在椭圆上,所以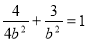 ,这样便得一方程组,解这个方程组求出a、b的值,即可得椭圆C的方程;(2)首先考虑直线MN垂直于
,这样便得一方程组,解这个方程组求出a、b的值,即可得椭圆C的方程;(2)首先考虑直线MN垂直于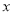 轴的情况,易得此时交点为
轴的情况,易得此时交点为 ,由此可知,点G的横坐标应当为8.当直线MN不垂直
,由此可知,点G的横坐标应当为8.当直线MN不垂直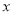 轴时,设直线MN:
轴时,设直线MN: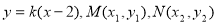 ,
,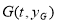 .由A、N、G三点共线有
.由A、N、G三点共线有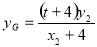 ,由A、N、G三点共线有
,由A、N、G三点共线有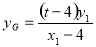 ,有
,有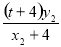
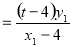 ,即
,即
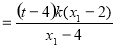 ,化简
,化简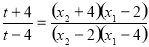 ,当
,当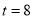 时化简得
时化简得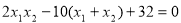 .接下来联立直线MN与椭圆方程再用韦达定理代入此等式验证即可.
.接下来联立直线MN与椭圆方程再用韦达定理代入此等式验证即可.
(1)由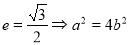 ,又点
,又点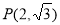 在椭圆上,所以
在椭圆上,所以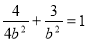 解得
解得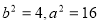 ,则椭圆C方程是
,则椭圆C方程是 ; .3分
; .3分
(2)当直线MN垂直于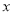 轴,交点为
轴,交点为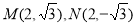 ,
,
由题知直线AN: ,直线MB:
,直线MB: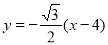 ,交点
,交点 .5分
.5分
当直线MN不垂直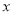 轴时,设直线MN:
轴时,设直线MN: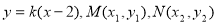 ,
,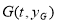
联立直线MN与椭圆方程得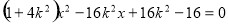
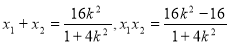 , .7分
, .7分
因为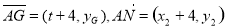 ,由A、N、G三点共线有
,由A、N、G三点共线有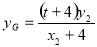
同理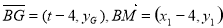 ,由A、N、G三点共线有
,由A、N、G三点共线有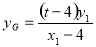
有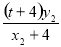
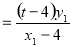 ,即
,即
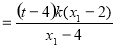 ,化简
,化简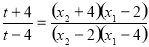 ,验证当
,验证当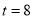 时化简得
时化简得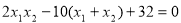 带入韦达定理恒成立,因此G的横坐标的值为8. 13分
带入韦达定理恒成立,因此G的横坐标的值为8. 13分
考点:1、轨迹方程的求法;2、直线与圆锥曲线的关系.


科目:高中数学 来源: 题型:
| A、5 | B、6 | C、7 | D、8 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三第六期3月阶段性考试文科数学试卷(解析版) 题型:选择题
若抛物线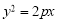 的焦点与双曲线
的焦点与双曲线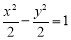 的右焦点重合,则
的右焦点重合,则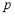 的值为( )
的值为( )
A.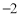 B.
B. C.
C.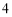 D.
D.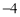
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三二诊模拟文科数学试卷(解析版) 题型:选择题
已知 是不重合的直线,
是不重合的直线,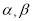 是不重合的平面,有下列命题:
是不重合的平面,有下列命题:
①若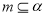 ,
, ∥
∥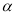 ,则
,则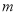 ∥
∥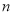 ;
;
②若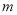 ∥
∥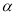 ,
, ∥
∥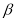 ,则
,则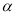 ∥
∥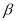 ;
;
③若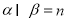 ,
,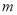 ∥
∥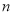 ,则
,则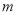 ∥
∥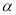 且
且 ∥
∥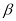 ;
;
④若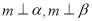 ,则
,则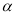 ∥
∥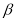
其中真命题的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com