
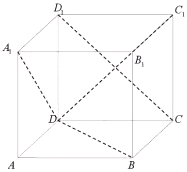
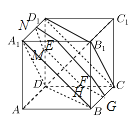
【题目】如图,![]() 的棱长为1的正方体,任作平面
的棱长为1的正方体,任作平面![]() 与对角线
与对角线![]() 垂直,使得
垂直,使得![]() 与正方体的每个面都有公共点,这样得到的截面多边形的面积为
与正方体的每个面都有公共点,这样得到的截面多边形的面积为![]() ,周长为
,周长为![]() 的范围分别是_____________(用集合表示)
的范围分别是_____________(用集合表示)
【答案】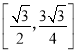 ;
;![]()
【解析】
由线面垂直的性质可知截面多边形的边与所在的正方形的对角线平行,利用相似比即可求得截面周长为定值.
连接![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]()
![]() ,又
,又![]()
![]() 平面
平面![]() ,
,![]()
同理可证![]()
则![]() 平面
平面![]() ,
,
设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
则![]() ,又
,又![]() ,
,
![]() ,
,
同理可得平面![]() 与其他各面的交线都与此平面的对角线平行,
与其他各面的交线都与此平面的对角线平行,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
同理可得六边形其他相邻两边的和为![]() ,
,
![]() 六边形的周长
六边形的周长![]() 为定值
为定值![]() .
.
因为截面与各面的交线与各面的对角线平行,所以不管六边形如何变化,六边形的每个内角都是![]() ,并且相邻边长的和为
,并且相邻边长的和为![]() ,通过构造边长为
,通过构造边长为![]() 的菱形,并且有一个角为
的菱形,并且有一个角为![]() ,
,
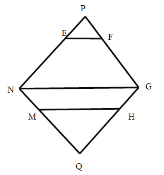
六边形![]() 的面积是如图两个等边三角形的面积减上下两个等边三角形的面积,
的面积是如图两个等边三角形的面积减上下两个等边三角形的面积,![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() ,
,
![]()
所以截面多边形面积的取值范围是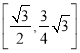
故答案为: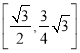 ;
;![]()


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足条件
满足条件![]() ,且
,且![]()
(1)计算![]() ,请猜测数列
,请猜测数列![]() 的通项公式,并用数学归纳法证明;
的通项公式,并用数学归纳法证明;
(2)请分别构造一个二阶和三阶行列式,使它们的值均为![]() ,其中,要求所构造的三阶行列式主对角线下方的元素均为零,并用按某行或者某列展开的方法验证三阶行列式的值为
,其中,要求所构造的三阶行列式主对角线下方的元素均为零,并用按某行或者某列展开的方法验证三阶行列式的值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.“![]() ”是“
”是“![]() ”充分的条件;
”充分的条件;
B.“![]() ”是“
”是“![]() ”成立的充分不必要条件;
”成立的充分不必要条件;
C.命题“已知![]() ,
,![]() 是实数,若
是实数,若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
D.命题“若![]() ,
,![]() 都是正数,则
都是正数,则![]() 也是正数”的逆否命题是“若
也是正数”的逆否命题是“若![]() 不是正数,则
不是正数,则![]() ,
,![]() 都不是正数”.
都不是正数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店为了了解销售单价(单位:元)在![]() 内的图书销售情况,从2018年上半年已经销售的图书中随机抽取100本,获得的所有样本数据按照
内的图书销售情况,从2018年上半年已经销售的图书中随机抽取100本,获得的所有样本数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图,已知样本中销售单价在
分成6组,制成如图所示的频率分布直方图,已知样本中销售单价在![]() 内的图书数是销售单价在
内的图书数是销售单价在![]() 内的图书数的2倍.
内的图书数的2倍.
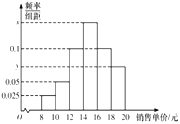
(1)求出x与y,再根据频率分布直方图佔计这100本图书销售单价的平均数、中位数(同一组中的数据用该组区间的中点值作代表);
(2)用分层抽样的方法从销售单价在![]() 内的图书中共抽取40本,求单价在6组样本数据中的图书销售的数量;
内的图书中共抽取40本,求单价在6组样本数据中的图书销售的数量;
(3)从(2)中抽取且价格低于12元的书中任取2本,求这2本书价格都不低于10元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出的是某高校土木工程系大四年级55名学生期末考试专业成绩的频率分布折线图(连接频率分布直方图中各小长方形上端的中点),其中组距为10,且本次考试中最低分为50分,最高分为100分.根据图中所提供的信息,则下列结论中正确的是( )

A. 成绩是75分的人数有20人
B. 成绩是100分的人数比成绩是50分的人数多
C. 成绩落在70-90分的人数有35人
D. 成绩落在75-85分的人数有35人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的侧面展开图是一个半圆.

(1)求圆锥的母线与底面所成的角;
(2)过底面中心![]() 且平行于母线
且平行于母线![]() 的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为
的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为![]() 的抛物线,求圆锥的全面积;
的抛物线,求圆锥的全面积;
(3)过底面点![]() 作垂直且于母线
作垂直且于母线![]() 的截面,若截面与圆锥侧面的交线是长轴为
的截面,若截面与圆锥侧面的交线是长轴为![]() 的椭圆,求椭圆的面积(椭圆号
的椭圆,求椭圆的面积(椭圆号![]() 的面积
的面积![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列, ![]() 公比为
公比为![]()
![]() 为数列{an}的前n项和.
为数列{an}的前n项和.
(1)若![]() 求
求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数n,不等式
,使得对任意正整数n,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y的焦点F和点A(-1,8),点P为抛物线上一点,则|PA|+|PF|的最小值为( )
A. 16 B. 6 C. 12 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
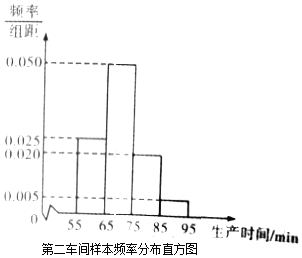
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com