
【题目】已知抛物线![]() 与直线
与直线![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:![]() ;
;
(2)当![]() 的面积等于
的面积等于![]() 时,求k的值.
时,求k的值.
【答案】解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意, ………… 2分
∴k 0由y =" k" (x+1)得x =![]() –1 代入y 2=" –" x 整理得: y 2+
–1 代入y 2=" –" x 整理得: y 2+![]() y – 1 =" 0" , 2分
y – 1 =" 0" , 2分
设A (x 1, y 1), B (x 2, y 2) 则y 1+ y 2= –![]() , y 1y 2=" –1." ………… 2分
, y 1y 2=" –1." ………… 2分
∵A、B在y 2=" –" x上, ∴A (–![]() , y 1), B (–
, y 1), B (–![]() , y 2) ,
, y 2) ,
∴ kOA·kOB=![]() =
=![]() =" –" 1 .
=" –" 1 .
∴ OA^OB. …………… 3 分
(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴|OE| =" 1" ,
【解析】
试题(1)可假设![]() ,分别代入抛物线方程与直线方程,化简整理可得
,分别代入抛物线方程与直线方程,化简整理可得![]() ,
,![]() ,利用向量垂直有
,利用向量垂直有![]() ,即证明
,即证明![]() ;(2)直线
;(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 的坐标为
的坐标为![]() ,则可将三角形
,则可将三角形![]() 拆为两个三角形
拆为两个三角形![]() ,两三角形具有相同的底边
,两三角形具有相同的底边![]() ,高分别为
,高分别为![]() 的纵坐标,利用(1)中
的纵坐标,利用(1)中![]() 的关系便可求得
的关系便可求得![]() 的面积函数,根据函数值求
的面积函数,根据函数值求![]() 的值.
的值.
试题解析:(1)证明:联立![]() ,消去x,得ky2+y-k=0.设A(x1,y1),B(x2,y2),则y1+y2=-
,消去x,得ky2+y-k=0.设A(x1,y1),B(x2,y2),则y1+y2=-![]() ,y1·y2=-1.因为y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即
,y1·y2=-1.因为y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即![]() =0,所以OA⊥OB.
=0,所以OA⊥OB.
(2)设直线l与x轴的交点为N,则N的坐标为(-1,0),
所以S△AOB=![]() |ON|·|y1-y2|
|ON|·|y1-y2|
=![]() ×|ON|×
×|ON|×![]()
=![]() ×1×
×1×![]() =
=![]() ,
,
解得k2=![]() ,所以k=±
,所以k=±![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知:等比数列{![]() }中,公比为q,且a1=2,a4=54,等差数列{
}中,公比为q,且a1=2,a4=54,等差数列{![]() }中,公差为d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
}中,公差为d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)求数列{![]() }的前n项和
}的前n项和![]() 的公式;
的公式;
(III)设![]() ,
,![]() ,其中n=1,2,…,试比较
,其中n=1,2,…,试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市民众对某项公共政策的态度,在该市随机抽取了![]() 名市民进行调查,做出了他们的月收入(单位:百元,范围:
名市民进行调查,做出了他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
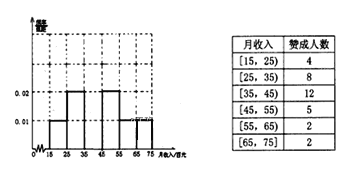
(1)求月收入在![]() 内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
(2)根据频率分布直方图估计这![]() 人的平均月收入;
人的平均月收入;
(3)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人,求
人,求![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是椭圆
是椭圆![]() 的左焦点,点
的左焦点,点![]() 是
是![]() 轴上的一点,点
轴上的一点,点![]() 为椭圆的左、右顶点,已知
为椭圆的左、右顶点,已知![]() ,且
,且![]()
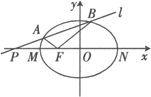
(1)求椭圆的标准方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,试判定直线
两点,试判定直线![]() 的斜率之和
的斜率之和![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若点D在边BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn= ![]() ,数列{cn}的前n项和为Tn=
,数列{cn}的前n项和为Tn= ![]() .求n.
.求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 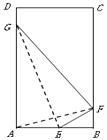
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com