练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出，需要设计各面是玻璃平面的无底正四棱柱将其罩住，罩内充满保护文物的无色气体.已知文物近似于塔形，高1.8米，体积0.5立方米，其底部是直径为0.9米的圆形，要求文物底部与玻璃罩底边至少间隔0.3米，文物顶部与玻璃罩上底面至少间隔0.2米，气体每立方米1000元，则气体费用最少为（ ）元

    A.4500B.4000C.2880D.2380

    【答案】B

    【解析】

    根据题意,先求得正四棱柱的底面棱长和高,由体积公式即可求得正四棱柱的体积.减去文物的体积,即可求得罩内的气体体积,进而求得所需费用.

    由题意可知, 文物底部是直径为0.9米的圆形,文物底部与玻璃罩底边至少间隔0.3米

    所以由正方形与圆的位置关系可知,底面正方形的边长为

    文物高1.8米,文物顶部与玻璃罩上底面至少间隔0.2米

    所以正四棱柱的高为

    则正四棱柱的体积为

    因为文物体积为

    所以罩内空气的体积为

    气体每立方米元

    所以共需费用为元

    故选:B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知位数满足下列条件：①各个数字只能从集合中选取；②若其中有数字，则在的前面不含，将这样的位数的个数记为；

    （1）求、；

    （2）探究与之间的关系，求出数列的通项公式；

    （3）对于每个正整数，在与之间插入个得到一个新数列，设是数列的前项和，试探究能否成立，写出你探究得到的结论并给出证明；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中a为非零常数．

    讨论的极值点个数，并说明理由；

    若，证明：在区间内有且仅有1个零点；设为的极值点，为的零点且，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）若，求曲线在处的切线方程;

    （2）设函数若至少存在一个,使得成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数据是郑州市普通职工个人的年收入，若这个数据的中位数为，平均数为，方差为，如果再加上世界首富的年收入，则这个数据中，下列说法正确的是（ ）

    A.年收入平均数大大增大，中位数一定变大，方差可能不变

    B.年收入平均数大大增大，中位数可能不变，方差变大

    C.年收入平均数大大增大，中位数可能不变，方差也不变

    D.年收入平均数可能不变，中位数可能不变，方差可能不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （I）试判断函数的单调性；

    （Ⅱ）若函数在上有且仅有一个零点，

    （i）求证：此零点是的极值点；

    （ⅱ）求证：.

    （本题可能会用到的数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调区间；

    （2）若函数的导函数在上有三个零点，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数

    (1)讨论函数的单调性；

    (2)若是的极值点，且曲线在两点， 处的切线互相平行，这两条切线在y轴上的截距分别为、，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，，直线l与椭圆C交于P，Q两点，且点M满足.

    （1）若点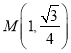，求直线的方程；

    （2）若直线l过点且不与x轴重合，过点M作垂直于l的直线与y轴交于点，求实数t的取值范围.

    查看答案和解析>>

    同步练习册答案