练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知实数1，m，16构成一个等比数列，则圆锥曲线x2+$\frac{{y}^{2}}{m}$=1的离心率为$\frac{\sqrt{3}}{2}$或$\sqrt{5}$．

    分析 由1，m，16构成一个等比数列，得到m=±4．当m=4时，圆锥曲线是椭圆；当m=-4时，圆锥曲线是双曲线，由此入手能求出离心率．

    解答 解：∵1，m，16构成一个等比数列，
    ∴m=±4．
    当m=4时，圆锥曲线x2+$\frac{{y}^{2}}{m}$=1是椭圆，它的离心率是$\frac{\sqrt{3}}{2}$；
    当m=-4时，圆锥曲线x2+$\frac{{y}^{2}}{m}$=1是双曲线，它的离心率是$\sqrt{5}$．
    故答案为：$\frac{\sqrt{3}}{2}$或$\sqrt{5}$．

    点评 本题考查圆锥曲线的离心率的求法，解题时要注意等比数列的性质的合理运用，注意分类讨论思想的灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．下列各组中的两个函数是同一函数的为（　　）
    A．f（x）=1，g（x）=x0B．f（x）=$\root{3}{x}$，g（x）=$\frac{{x}^{2}}{x}$C．f（x）=lnex，g（x）=elnxD．f（x）=$\frac{1}{|x|}$，g（x）=$\frac{1}{\sqrt{{x}^{2}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知$|\overrightarrow a|$=$|\overrightarrow b|$=2，且它们的夹角为$\frac{π}{3}$，则$|\overrightarrow a+\overrightarrow b|$=（　　）
    A．$2\sqrt{3}$B．$3\sqrt{2}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．圆x2+y2+4x-2y-1=0上存在两点关于直线ax-2by+1=0（a＞0，b＞0）对称，则$\frac{1}{a}$+$\frac{4}{b}$的最小值为（　　）
    A．3+2$\sqrt{2}$B．9C．16D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．如图是甲，乙两名同学5次综合测评成绩的茎叶图，甲乙两人中成绩较为稳定的是甲

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在长方体ABCD-A1B1C1D1中，AA1=AD=4，E是棱CD上的一点．
    （1）求证：AD1⊥平面A1B1D；
    （2）求证：B1E⊥AD1；
    （3）若E是棱CD的中点，在棱AA1上是否存在点P，使得DP∥平面B1AE？若存在，求出线段AP的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={x||x-2|＜3，x∈Z}，B={0，1，2}，则集合A∩B=（　　）
    A．{0，1，2}B．{0，1，2，3}C．{0，1}D．{1，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

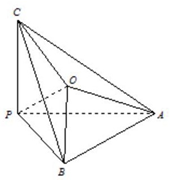    12．如图，在三棱锥P-ABC中，∠APB=∠BPC=∠APC=90°，O在△ABC内，∠OPC=45°，∠OPA=60°，则∠OPB的余弦值为（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{6}}{3}$C．$\frac{1}{2}$D．$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知f（x）为偶函数，f（2+x）=f（2-x），当-2≤x≤0时，f（x）=2x，则f（2011）=$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案