
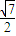 ),N(-
),N(-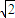 ,
,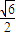 ),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.
),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.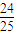 =0恒有公共点,试求m的取值范围.
=0恒有公共点,试求m的取值范围.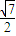 ),N(-
),N(-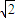 ,
,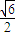 ),所以可得
),所以可得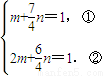
 ,由此能求出抛物线方程与椭圆的标准方程.
,由此能求出抛物线方程与椭圆的标准方程.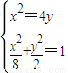 得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),当y=1时,得x=±2,因为xA<xB,所以A(-2,1),对y=
得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),当y=1时,得x=±2,因为xA<xB,所以A(-2,1),对y= x2求导,得y′=
x2求导,得y′= x,所以直线l′的方程为x+y+1=0,由此能求出直线l′与坐标轴所围成的三角形的面积.
x,所以直线l′的方程为x+y+1=0,由此能求出直线l′与坐标轴所围成的三角形的面积.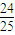 =0得(x-m)2+(y+1)2=
=0得(x-m)2+(y+1)2=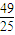 ,其圆心坐标为(m,-1),半径r=
,其圆心坐标为(m,-1),半径r=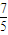 ,要使直线l′与圆x2-2mx+y2+2y+m2-
,要使直线l′与圆x2-2mx+y2+2y+m2-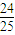 =0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤
=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤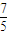 ,由此能求出m的取值范围.
,由此能求出m的取值范围.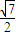 ),N(-
),N(-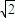 ,
,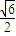 ),
),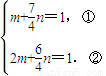
 ,③
,③ ,
,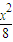 +
+ =1.
=1.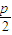 ),依题意得直线FP与直线l:x-y-2=0互相垂直,所以直线FP的斜率为-1,则kFP=
),依题意得直线FP与直线l:x-y-2=0互相垂直,所以直线FP的斜率为-1,则kFP=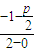 =-1,解得p=2,所以x2=4y.
=-1,解得p=2,所以x2=4y.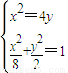 得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),
得y2+y-2=0,解得y=1或y=-2(不合题意,舍去), x2求导,得y′=
x2求导,得y′= x,所以y′|x=-2=-1,所以直线l′的方程为y-1=-1×(x+2),即x+y+1=0,令x=0得y=-1,令y=0得x=-1,所以直线l′与坐标轴所围成的三角形的面积为S=
x,所以y′|x=-2=-1,所以直线l′的方程为y-1=-1×(x+2),即x+y+1=0,令x=0得y=-1,令y=0得x=-1,所以直线l′与坐标轴所围成的三角形的面积为S= ×|-1|×|-1|=
×|-1|×|-1|= .
. =0得(x-m)2+(y+1)2=
=0得(x-m)2+(y+1)2=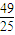 ,其圆心坐标为(m,-1),半径r=
,其圆心坐标为(m,-1),半径r=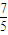 ,
,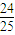 =0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤
=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤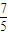 ,即d=
,即d=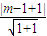 ≤
≤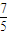 ,得-
,得-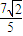 ≤m≤
≤m≤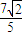 ,
,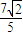 ,
,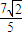 ].
].

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| AF |
| FB |
| AB |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
|
|
|
| ||
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com