
 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
分析 模拟程序的运行,依次写出每次循环得到的e,n的值,当n=5时满足条件退出循环,输出e的值即可得解.
解答 解:模拟程序的运行,可得
?=0.01,e=1,n=1
执行循环体,e=2,n=2
不满足条件$\frac{1}{n!}$<?,执行循环体,e=2+0.5=2.5,n=3
不满足条件$\frac{1}{n!}$<?,执行循环体,e=2.5+$\frac{1}{6}$,n=4
不满足条件$\frac{1}{n!}$<?,执行循环体,e=2.5+$\frac{1}{6}$+$\frac{1}{24}$,n=5
由于$\frac{1}{5!}$≈0.008<?=0.01,满足条件$\frac{1}{n!}$<?,退出循环,输出e的值为2.5+$\frac{1}{6}$+$\frac{1}{24}$=2.71.
故选:C.
点评 本题考查的知识点是程序框图,在写程序的运行结果时,我们常使用模拟循环的变法,但程序的循环体中变量比较多时,要用表格法对数据进行管理,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 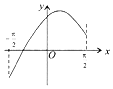 | B. | 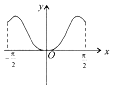 | C. | 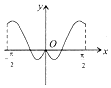 | D. | 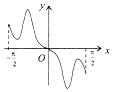 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {0,1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 水果产量(kg) | 3000 | 4000 |
| 概率 | 0.4 | 0.6 |
| 水果市场价格(元/kg) | 16 | 20 |
| 概率 | 0.5 | 0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com