
分析 (1)设直线方程为y=k(x+2),与直线l1:y=2x,l2:y=-2x,分别联立,可得A,B的纵坐标,再由△NAB的面积为$\frac{1}{2}$|MN|•(yB-yA)=16,解方程可得k,进而得到所求直线方程;
(2)求得A,B的坐标,设P(a,-2a),Q(b,2b),运用三点共线的条件:斜率相等,求得a,b,再由两点的斜率公式,化简整理,计算即可得到所求定值.
解答 解:(1)设直线方程为y=k(x+2),
与直线l1:y=2x,l2:y=-2x,分别联立,
可得A,B的纵坐标分别为$\frac{4k}{2-k}$,$\frac{4k}{k+2}$,
∵△NAB的面积为16,
∴$\frac{1}{2}$|MN|•(yB-yA)=16,
即$\frac{1}{2}×3×$($\frac{4k}{k+2}$-$\frac{4k}{2-k}$)=16,
解得k=±4,
∴直线l的方程为4x±y+8=0;
(2)由(1)可得A($\frac{2{k}_{1}}{2-{k}_{1}}$,$\frac{4{k}_{1}}{2-{k}_{1}}$),B(-$\frac{2{k}_{1}}{2+{k}_{1}}$,$\frac{4{k}_{1}}{2+{k}_{1}}$),
又N(1,0),设P(a,-2a),Q(b,2b),
由A,N,P共线,可得
$\frac{2a}{1-a}$=$\frac{4{k}_{1}}{3{k}_{1}-2}$,解得a=$\frac{2{k}_{1}}{5{k}_{1}-2}$,
即有P($\frac{2{k}_{1}}{5{k}_{1}-2}$,-$\frac{4{k}_{1}}{5{k}_{1}-2}$),
由B,N,Q共线,可得
$\frac{2b}{b-1}$=$\frac{4{k}_{1}}{-3{k}_{1}-2}$,解得b=$\frac{2{k}_{1}}{5{k}_{1}+2}$,
即有Q($\frac{2{k}_{1}}{5{k}_{1}+2}$,$\frac{4{k}_{1}}{5{k}_{1}+2}$),
则k2=$\frac{\frac{4{k}_{1}}{5{k}_{1}+2}-\frac{-4{k}_{1}}{5{k}_{1}-2}}{\frac{2{k}_{1}}{5{k}_{1}+2}-\frac{2{k}_{1}}{5{k}_{1}-2}}$=-5k1,
即有$\frac{k_1}{k_2}$为定值-$\frac{1}{5}$.
点评 本题考查直线方程的求法,注意运用待定系数法,考查直线交点问题注意联立方程,考查三点共线的条件:斜率相等,以及斜率公式的运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
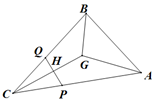 如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )
如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| B. | “x=1”是“x2-3x+2=0”的充分必要条件. | |
| C. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”是真命题 | |
| D. | 若¬(p∧q)为真命题,则p、q至少有一个为假命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.
如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com