
【题目】如图,已知函数![]() 的图象与y轴交于点
的图象与y轴交于点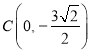 ,与x轴交于A,B两点,其中
,与x轴交于A,B两点,其中![]() ,
,![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,求证:
,求证:![]() 的外接圆恒过原点
的外接圆恒过原点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线
,准线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.
![]() 若
若![]() ,
,![]() ,求直线
,求直线![]() 的方程;
的方程;
![]() 若
若![]() ,点
,点![]() 为准线
为准线![]() 上任意一点,求证:直线
上任意一点,求证:直线![]() ,
,![]() ,
,![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校甲、乙、丙、丁四个专业分别有150,150,400,300名学生.为了解学生的就业倾向,用分层抽样的方法从该校这四个专业中抽取60名学生进行调查,则应从丁专业抽取的学生人数为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: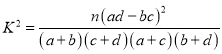 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确领导下,通过全国人民的齐心协力,特别是全体一线医护人员的共同努力,新冠肺炎疫情得到了有效控制.作为集中医学观察隔离点的某酒店在疫情期间,为客人提供两种速食品—“方便面”和“自热米饭”.为调查这两种速食品的受欢迎程度,酒店部门经理记录了连续10天这两种速食品的销售量,得到如下频数分布表(其中销售量单位:盒):
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方便面 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 |
自热米饭 | 88 | 96 | 98 | 97 | 101 | 99 | 102 | 107 | 104 | 112 |
(1)根据两组数据完成下面的茎叶图(填到答题卡上);

(2)根据统计学知识,你认为哪种速食品更受欢迎,并简要说明理由;
(3)求自热米饭销售量y关于天数t的线性回归方程,并预估第12天自热米饭的销售量(结果精确到整数).
参考数据:![]() ,
,![]() .
.
附:回归直线方程![]() ,其中
,其中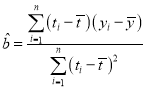 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
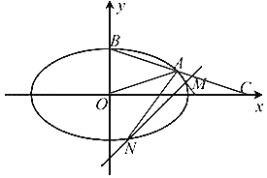
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于第一象限上的点,
上位于第一象限上的点,![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 过椭圆
过椭圆![]() 的右焦点,且与椭圆
的右焦点,且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 在直线
在直线![]() 的同侧),若
的同侧),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com