
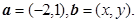
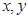 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.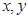 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足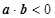 的概率.
的概率. ;(2)
;(2)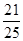 .
. 得
得 ,所以
,所以 所包含的基本事件为
所包含的基本事件为 ,所求的概率为
,所求的概率为 .
. 在连续区间[1,6]上取值,这符合几何概型的条件,事件的全部结果构成的区域
在连续区间[1,6]上取值,这符合几何概型的条件,事件的全部结果构成的区域 ,满足
,满足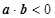 基本事件的结果为
基本事件的结果为 ,
,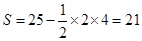 ,所求概率
,所求概率 .
. 有-2x+y=-1,所以满足
有-2x+y=-1,所以满足 的基本事件为(1,1),(2,3),(3,5),共3个;故满足
的基本事件为(1,1),(2,3),(3,5),共3个;故满足 的概率为
的概率为 =
= .
.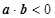 的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};画出图形如下图,
的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};画出图形如下图,
 ×2×4=21,
×2×4=21,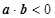 的概率为
的概率为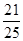 .
.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:不详 题型:解答题
 、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com