
【题目】已知等差数列{an}满足a3=7,a5+a7=26,数列{an}的前n项和Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
科目:高中数学 来源: 题型:
【题目】【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1:几何证明选讲
如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M.
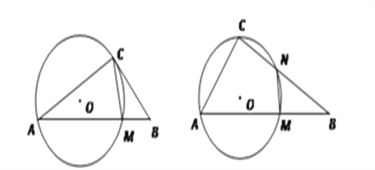
(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
C.选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l: 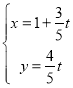 (t为参数),与曲线C:
(t为参数),与曲线C: 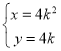 (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
D.选修4—5:不等式选讲
设a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知 a>0 且 a≠1,若函数f(x)=loga(x﹣1),g(x)=loga(5﹣x).
(1)求函数h(x)=f(x)﹣g(x)的定义域;
(2)讨论不等式f(x)≥g(x)成立时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,符号[x]表示不超过x的最大整数,如[2.2]=2,[﹣3.5]=﹣4,设数列{an}的通项公式为an=[log21]+[log22]+[log23]+…[log2(2n﹣1)].
(1)求a1a2a3的值;
(2)是否存在实数a,使得an=(n﹣2)2n+a(n∈N*),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生产甲乙两种精密电子产品,用以下两种方案分别生产出甲乙产品共![]() 种,现对这两种方案生产的产品分别随机调查了各
种,现对这两种方案生产的产品分别随机调查了各![]() 次,得到如下统计表:
次,得到如下统计表:
①生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
频 数 |
|
|
|
|
|
|
②生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
频 数 |
|
|
|
|
|
|
已知生产电子产品甲![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元;生产电子产品乙
元;生产电子产品乙![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元.
元.
(I)按方案①生产![]() 件甲产品和
件甲产品和![]() 件乙产品,求这
件乙产品,求这![]() 件产品平均利润的估计值;
件产品平均利润的估计值;
(II)从方案①②中选其一,生产甲乙产品共![]() 件,欲使
件,欲使![]() 件产品所得总利润大于
件产品所得总利润大于![]() 元的机会多,应选用哪个?
元的机会多,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣kx,x∈R(e是自然对数的底数).
(1)若k∈R,求函数f(x)的单调区间;
(2)若k>0,讨论函数f(x)在(﹣∞,4]上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x+2y+m=0与y轴交于A,B两点,且∠ACB=90°(C为圆心),过点P(0,2)且斜率为k的直线与圆C相交于M,N两点.
(1)求实数m的值;
(2)若|MN|≥4,求k的取值范围;
(3)若向量 ![]() 与向量
与向量 ![]() 共线(O为坐标原点),求k的值.
共线(O为坐标原点),求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的四个小球,它们的标号分别为1、2、3、4,现从袋中不放回地随机抽取两个小球,记第一次取出的小球的标号为a,第二次取出的小球的标号为b,记事件A为“a+b≥6“.
(1)列举出所有的基本事件(a,b),并求事件A的概率P(A);
(2)在区间[0,2]内任取两个实数x,y,求事件“x2+y2≥12P(A)“的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在以极点为直角坐标原点
,在以极点为直角坐标原点![]() ,极轴为
,极轴为![]() 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为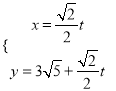 (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,设曲线![]() 经过伸缩变换
经过伸缩变换![]() :
: 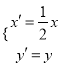 得到曲线
得到曲线![]() ,若
,若![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com