
四面体ABCD中,设M是CD的中点,则 化简的结果是( )
化简的结果是( )
A.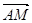 | B. | C. | D.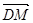 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
下列命题正确的是( ).
A.若a、b都是单位向量,则a=b
B.向量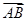 与
与 是两平行向量
是两平行向量
C.若 ,则A、B、C、D四点构成平行四边形
,则A、B、C、D四点构成平行四边形
D.两向量相等的充要条件是它们的始点和终点相同
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设 ,
, ,
,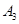 ,
, 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称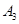 ,
, 调和分割
调和分割 ,
, ,已知点C(c,0),
,已知点C(c,0),
D(d,0) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
| A.C可能是线段AB的中点 | B.D可能是线段AB的中点 |
| C.C,D可能同时在线段AB上 | D.C,D不可能同时在线段AB的延长线上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com