
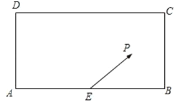
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m、n 是两条不同的直线,α、β、γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β , β⊥γ ,则α∥γ
B.若 ![]() ,
, ![]() , m∥n ,则α∥β
, m∥n ,则α∥β
C.若 m、n 是异面直线, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,则α∥β
, n∥α ,则α∥β
D.平面α内有不共线的三点到平面 β的距离相等,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
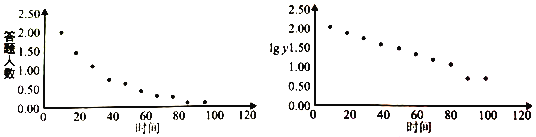
【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: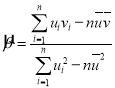 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长四尺,莞生一日,长一尺.蒲生日自半,莞生日自倍.意思是:今有蒲第一天长高四尺,莞第一天长高一尺,以后蒲每天长高前一天的一半,莞每天长高前一天的两倍.请问第几天,莞的长度是蒲的长度的4倍( )
A.4天B.5天C.6天D.7天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来就一直使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字开始,“地支”以“子”字开始,两者按照干支顺序相配,构成了“干支纪年法”,其相配顺序为:甲子、乙丑、丙寅![]() 癸酉、甲戌、乙亥、丙子
癸酉、甲戌、乙亥、丙子![]() 癸未、甲申、乙酉、丙戌
癸未、甲申、乙酉、丙戌![]() 癸巳
癸巳![]() 癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
A.甲巳年B.壬辰年C.癸巳年D.辛卯年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率
的离心率![]() ,椭圆C上的点到其左焦点的最大距离为
,椭圆C上的点到其左焦点的最大距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A![]() 作直线
作直线![]() 与椭圆相交于点B,则
与椭圆相交于点B,则![]() 轴上是否存在点P,使得线段
轴上是否存在点P,使得线段![]() ,且
,且![]() ?若存在,求出点P坐标;否则请说明理由.
?若存在,求出点P坐标;否则请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com