
【题目】已知函数![]() ,点
,点![]() 和
和![]() 是函数
是函数![]() 图像的相邻的两个对称中心,且函数
图像的相邻的两个对称中心,且函数![]() 在区间
在区间![]() 内单调递减,则
内单调递减,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某科研团队对某一生物生长规律进行研究,发现其生长蔓延的速度越来越快.开始在某水域投放一定面积的该生物,经过2个月其覆盖面积为18平方米,经过3个月其覆盖面积达到27平方米.该生物覆盖面积![]() (单位:平方米)与经过时间
(单位:平方米)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(1)试判断哪个函数模型更合适,并求出该模型的函数解析式;
(2)问约经过几个月,该水域中此生物的面积是当初投放的1000倍![]() (参考数据:
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮,中国华为公司研发的![]() 、
、![]() 两种芯片都已获得成功.该公司研发芯片已经耗费资金
两种芯片都已获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产,经市场调查与预测,生产
千万元,现在准备投入资金进行生产,经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() (
(![]() 与
与![]() 都为常数),其图象如图所示.
都为常数),其图象如图所示.
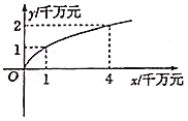
(1)试分别求出生产![]() 、
、![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式;
(千万元)函数关系式;
(2)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() 、
、![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所获利润,当
表示公司所获利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
(2)能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 所示,一条直角走廊宽为
所示,一条直角走廊宽为![]() ,
,![]()


(1)若位于水平地面上的一根铁棒在此直角走廊内,且![]() ,试求铁棒的长
,试求铁棒的长![]() ;
;
(2)若一根铁棒能水平地通过此直角走廊,求此铁棒的最大长度;
(3)现有一辆转动灵活的平板车,其平板面是矩形,它的宽![]() 为
为![]()
![]() 如图2.平板车若想顺利通过直角走廊,其长度
如图2.平板车若想顺利通过直角走廊,其长度![]() 不能超过多少米?
不能超过多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com