
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,线段
,线段![]() 的长为4.点
的长为4.点![]() 在椭圆
在椭圆![]() 上且位于第一象限,过点
上且位于第一象限,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
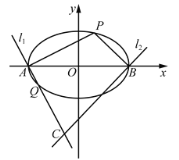
(1)若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点为
的另一交点为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先求出椭圆的方程,设直线![]() 的方程为
的方程为![]() .分别表示出直线
.分别表示出直线![]() 与
与![]() 的方程,联立方程组,求出点
的方程,联立方程组,求出点![]() 的坐标,利用点
的坐标,利用点![]() 的横坐标为
的横坐标为![]() ,求出
,求出![]() ,进而可求出点
,进而可求出点![]() 的坐标;(2 )联立
的坐标;(2 )联立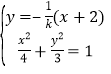 消去
消去![]() ,整理得
,整理得![]() ,求得
,求得![]() .由
.由![]() ,可得
,可得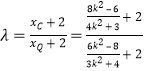
![]() ,结合
,结合![]() 即可求出
即可求出![]() 的取值范围.
的取值范围.
(1)设直线![]() 的斜率为
的斜率为![]() ,
,![]() ,
,
由题意得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
因为点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,
上,且位于第一象限,
所以![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
因为![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
联立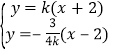 ,解得
,解得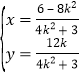 ,
,
即![]() .
.
因为![]() ,所以
,所以![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
因为![]() ,所以
,所以![]() .
.
则直线![]() 的方程为
的方程为![]() .
.
联立 ,解得
,解得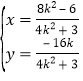 ,
,
即![]() .
.
因为点![]() 的横坐标为-1,
的横坐标为-1,
所以![]() ,解得
,解得![]() .
.
因为![]() ,
,
所以![]() .将
.将![]() 代入
代入![]() 可得,
可得,
点![]() 的坐标为
的坐标为![]() .
.
(2)设![]() ,
,![]() ,又直线
,又直线![]() 的方程为
的方程为![]() .
.
联立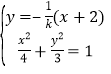 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,
解得![]() .
.
因为![]() ,
,
所以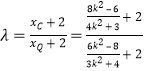
![]() .
.
因为![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名去参加会议,有多少种不同的选法?
(2)选出2名男教师或2名女教师去外地学习的选法有多少种?
(3)现要从中选出男、女老师各2名去参加会议,有多少种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节档有多部优秀电影上映,其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况,得到如下表格:
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况,试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率;
(2)以表中各评价等级对应的频率作为各评价等级对应的概率,假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名,求恰有2名评价为五星1名评价为一星的概率;
(ii)若从全国所有观众中随机选取16名,记评价为五星的人数为X,求X的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲箱中装有3个红球,2个黑球,乙箱中装有2个红球,3个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,规定顾客购物1000元以上,可以参与抽奖一次,设奖规则如下:每次分别从以上两个箱子中各随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,奖金300元;摸出的球中有3个红球,则获得二等奖,奖金200元;摸出的球中有2个红球,则获得三等奖,奖金100元;其他情况不获奖,每次摸球结束后将球放回原箱中.
(1)求在1次摸奖中,获得二等奖的概率;
(2)若3人各参与摸奖1次,求获奖人数X的数学期望![]() ;
;
(3)若商场同时还举行打9折促销活动,顾客只能在两项促销活动中任选一项参与.假若你购买了价值1200元的商品,那么你选择参与哪一项活动对你有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com