
【题目】定义在实数集上的函数f(x)=x2+ax(a为常数),g(x)= ![]() x3﹣bx+m(b为常数),若函数f(x)在x=1处的切线斜率为3,x=
x3﹣bx+m(b为常数),若函数f(x)在x=1处的切线斜率为3,x= ![]() 是g(x)的一个极值点
是g(x)的一个极值点
(1)求a,b的值;
(2)若存在x∈[﹣4,4]使得f(x)≥g(x)成立,求实数m的取值范围.
【答案】
(1)解:函数f(x)=x2+ax,f′(x)=2x+a,
若函数f(x)在x=1处的切线斜率为3,
则f′(1)=2+a=3,解得:a=1,
g(x)= ![]() x3﹣bx+m,g′(x)=x2﹣b,
x3﹣bx+m,g′(x)=x2﹣b,
若x= ![]() 是g(x)的一个极值点,
是g(x)的一个极值点,
则g′( ![]() )=2﹣b=0,解得:b=2
)=2﹣b=0,解得:b=2
(2)解:由(1)得:f(x)=x2+x,g(x)= ![]() x3﹣2x+m,
x3﹣2x+m,
令h(x)=g(x)﹣f(x)= ![]() x3﹣2x+m﹣x2﹣x=
x3﹣2x+m﹣x2﹣x= ![]() x3﹣3x+m﹣x2
x3﹣3x+m﹣x2
∴h′(x)=x2﹣2x﹣3,
当﹣4<x<﹣1时,h′(x)>0,
当﹣1<x<3时,h′(x)<0,
当3<x<4时,h′(x)>0,
要使f(x)≥g(x)恒成立,即h(x)max≤0,
由上知h(x)的最大值在x=﹣1或x=4取得,
而h(﹣1)=m+ ![]() ,h(4)=m﹣
,h(4)=m﹣ ![]() ,
,
∵m+ ![]() >m﹣
>m﹣ ![]() ,
,
∴m+ ![]() ≤0,
≤0,
即m≤﹣ ![]()
【解析】(1)分别求出f(x),g(x)的导数,根据f′(1)=0,g′( ![]() )=0,分别求出a,b的值即可;(2)令h(x)=g(x)﹣f(x),要使f(x)≥g(x)恒成立,即h(x)max≤0,转化为求最值问题.
)=0,分别求出a,b的值即可;(2)令h(x)=g(x)﹣f(x),要使f(x)≥g(x)恒成立,即h(x)max≤0,转化为求最值问题.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()
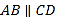
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log3(9x+1)+mx为偶函数,g(x)= ![]() 为奇函数.
为奇函数.
(Ⅰ)求m﹣n的值;
(Ⅱ)若函数y=f(x)与 ![]() 的图象有且只有一个交点,求实数a的取值范围.
的图象有且只有一个交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校食堂早餐只有花卷、包子、面条和蛋炒饭四种主食可供食用,有5名同学前去就餐,每人只选择其中一种,且每种主食都至少有一名同学选择.已知包子数量不足仅够一人食用,甲同学肠胃不好不会选择蛋炒饭,则这5名同学不同的主食选择方案种数为________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c且面积为S,满足S= ![]() bccosA
bccosA
(1)求cosA的值;
(2)若a+c=10,C=2A,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]()
(1)求f(x)在[1,m](m>1)上的最小值;
(2)若关于x的不等式f2(x)﹣nf(x)>0有且只有三个整数解,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设xOy,![]() 为两个平面直角坐标系,它们具有相同的原点,Ox正方向到
为两个平面直角坐标系,它们具有相同的原点,Ox正方向到![]() 正方向的角度为θ,那么对于任意的点M,在xOy下的坐标为(x,y),那么它在
正方向的角度为θ,那么对于任意的点M,在xOy下的坐标为(x,y),那么它在![]() 坐标系下的坐标(
坐标系下的坐标(![]() ,
,![]() )可以表示为:
)可以表示为:![]() =xcosθ+ysinθ,
=xcosθ+ysinθ,![]() =ycosθ-xsinθ.根据以上知识求得椭圆3
=ycosθ-xsinθ.根据以上知识求得椭圆3![]() -
-![]() +
+![]() -1=0的离心率为
-1=0的离心率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(sin 2x,1),B![]() ,设函数f(x)=
,设函数f(x)=![]() (x∈R),其中O为坐标原点.
(x∈R),其中O为坐标原点.
(1)求函数f(x)的最小正周期;
(2)当x∈![]() 时,求函数f(x)的最大值与最小值;
时,求函数f(x)的最大值与最小值;
(3)求函数f(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com