
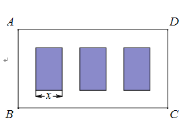
【题目】某广场要划出一块矩形区域![]() ,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设
,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设![]() 宽的走道,如图.已知三块园圃的总面积为
宽的走道,如图.已知三块园圃的总面积为![]() ,设园圃小矩形的一边长为
,设园圃小矩形的一边长为![]() ,区域
,区域![]() 的面积为
的面积为![]() (单位:
(单位:![]() ).
).
(1)求![]() 的最小值.
的最小值.
(2)若区域![]() 的面积不超过
的面积不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园内有一个以O为圆心,半径为5百米,圆心角为![]() 的扇形人工湖OAB,OM、ON是分别由OA、OB延伸而成的两条观光道.为便于游客观光,公园的主管部门准备在公园内增建三条观光道,其中一条与
的扇形人工湖OAB,OM、ON是分别由OA、OB延伸而成的两条观光道.为便于游客观光,公园的主管部门准备在公园内增建三条观光道,其中一条与![]() 相切点F,且与OM、ON分别相交于C、D,另两条是分别和湖岸OA、OB垂直的FG、FH (垂足均不与O重合).
相切点F,且与OM、ON分别相交于C、D,另两条是分别和湖岸OA、OB垂直的FG、FH (垂足均不与O重合).
(1) 求新增观光道FG、FH长度之和的最大值;
(2) 在观光道ON段上距离O为15百米的E处的道路两侧各有一个大型娱乐场,为了不影响娱乐场平时的正常开放,要求新增观光道CD的延长线不能进入以E为圆心,2.5百米为半径的圆形E的区域内.则点D应选择在O与E之间的什么位置?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机场建在一个海湾的半岛上,飞机跑道![]() 的长为
的长为![]() ,且跑道所在的直线与海岸线l的夹角为
,且跑道所在的直线与海岸线l的夹角为![]() (海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离
(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离![]() .D为海湾一侧海岸线
.D为海湾一侧海岸线![]() 上的一点,设
上的一点,设![]() (
(![]() ),点D对跑道
),点D对跑道![]() 的视角为
的视角为![]() .
.

(1)将![]() 表示为x的函数;
表示为x的函数;
(2)求点D的位置,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南![]() 镇2009~2018年梅雨季节的降雨量(单位:
镇2009~2018年梅雨季节的降雨量(单位:![]() )的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
)的频率分布直方图,试用样本频率估计总体概率,解答下列问题:

![]() “梅实初黄暮雨深”.请用样本平均数估计
“梅实初黄暮雨深”.请用样本平均数估计![]() 镇明年梅雨季节的降雨量;
镇明年梅雨季节的降雨量;
![]() “江南梅雨无限愁”.
“江南梅雨无限愁”.![]() 镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅2009~2018年的亩产量(
镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅2009~2018年的亩产量(![]() /亩)与降雨量的发生频数(年)如
/亩)与降雨量的发生频数(年)如![]() 列联表所示(部分数据缺失).请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅受降雨量影响更小?
列联表所示(部分数据缺失).请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅受降雨量影响更小?
(完善列联表,并说明理由).
亩产量\降雨量 |
|
| 合计 |
<600 | 2 | ||
| 1 | ||
合计 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在竖直坐标平面![]() 中,从坐标原点
中,从坐标原点![]() 出发以同一初速度
出发以同一初速度![]() 和不同的发射角(即发射方向与
和不同的发射角(即发射方向与![]() 轴正向之间的夹角)
轴正向之间的夹角)![]() 射出的质点(不计质点的大小),在重力(设重力加速度为
射出的质点(不计质点的大小),在重力(设重力加速度为![]() )的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线
)的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线![]() 在其上的点
在其上的点![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com