练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设 ， 为非零向量，则“存在负数λ，使得 =λ ”是 ＜0”的（　　）
    A.充分而不必要条件
    B.必要而不充分条件
    C.充分必要条件
    D.既不充分也不必要条件

    【答案】A
    【解析】解： ， 为非零向量，存在负数λ，使得 =λ ，则向量 ， 共线且方向相反，可得 ＜0．
    反之不成立，非零向量 ， 的夹角为钝角，满足 ＜0，而 =λ 不成立．
    ∴ ， 为非零向量，则“存在负数λ，使得 =λ ”是 ＜0”的充分不必要条件．
    故选：A．
    ， 为非零向量，存在负数λ，使得 =λ ，则向量 ， 共线且方向相反，可得 ＜0．反之不成立，非零向量 ， 的夹角为钝角，满足 ＜0，而 =λ 不成立．即可判断出结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点P是椭圆E:+y2=1上的任意一点,F1,F2是它的两个焦点,O为坐标原点,动点Q满足.

    (1)求动点Q的轨迹方程;

    (2)若已知点A(0,-2),过点A作直线l与椭圆E相交于B,C两点,求△OBC面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设圆的圆心在轴上，并且过两点.

    (1)求圆的方程；

    (2)设直线与圆交于两点，那么以为直径的圆能否经过原点，若能，请求出直线的方程；若不能，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正四棱台ABCD－A1B1C1D1中，上底面A1B1C1D1边长为1，下底面ABCD边长为2，侧棱与底面所成的角为60°，则异面直线AD1与B1C所成角的余弦值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x3﹣ ax2 ， a∈R，
    （1）当a=2时，求曲线y=f（x）在点（3，f（3））处的切线方程；
    （2）设函数g（x）=f（x）+（x﹣a）cosx﹣sinx，讨论g（x）的单调性并判断有无极值，有极值时求出极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

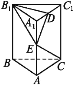
    【题目】如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30），[30，40），…[80，90]，并整理得到如下频率分布直方图：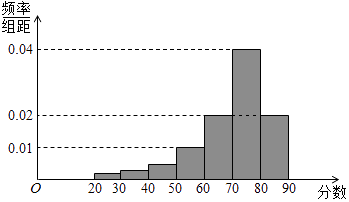

    （Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
    （Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50）内的人数；
    （Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB， = =2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（ ）

    A.γ＜α＜β
    B.α＜γ＜β
    C.α＜β＜γ
    D.β＜γ＜α

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD． 求证：（Ⅰ）EF∥平面ABC；
    （Ⅱ）AD⊥AC．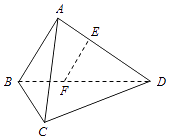

    查看答案和解析>>

    同步练习册答案