
【题目】命题p:函数f(x)= ![]() (a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0,
(a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0, ![]() ],x2﹣a≤0恒成立.
],x2﹣a≤0恒成立.
(1)求命题q真时a的取值范围;
(2)若命题p∧q为假,p∨q为真,求a的取值范围.
【答案】
(1)解:若命题q为真命题,
则a≥x2,x∈[0, ![]() ],恒成立,
],恒成立,
即a≥x2max,即 ![]() ;
;
(2)解:若函数f(x)= ![]() (a>0,
(a>0,
且a≠1)在R上为单调递减函数,
则 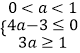 ,解得:
,解得: ![]() ≤a≤
≤a≤ ![]() ;
;
若命题p∧q为假,p∨q为真,
则命题p,q一真一假,
当p真q假时,a< ![]() 且
且 ![]() ≤a≤
≤a≤ ![]() ,解得:
,解得: ![]() ;
;
当p假q真时,a≤0,或a≥1,且 ![]() ,解得:
,解得: ![]() ;
;
综上可得: ![]() 或
或 ![]() .
.
【解析】(1)若命题q为真命题,则a≥x2 , x∈[0, ![]() ],恒成立,即a≥x2max;(2)若命题p∧q为假,p∨q为真,命题p,q一真一假,进而可得满足条件的a的取值范围.
],恒成立,即a≥x2max;(2)若命题p∧q为假,p∨q为真,命题p,q一真一假,进而可得满足条件的a的取值范围.
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和是Sn , 且Sn+ ![]() an=1(n∈N*).
an=1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log4(1﹣Sn+1)(n∈N*),Tn= ![]() +
+ ![]() +…+
+…+ ![]() ,求使Tn≥
,求使Tn≥ ![]() 成立的最小的正整数n的值.
成立的最小的正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=4
(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x﹣y+1=0与圆C交于A、B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2﹣a2= ![]() bc,且b=
bc,且b= ![]() a,则下列关系一定不成立的是( )
a,则下列关系一定不成立的是( )
A.a=c
B.b=c
C.2a=c
D.a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com