Question

¹⁰=a+a₁（x+1）+a₂（x+1）²+…+a₉（x+1）⁹+a₁₀（x+1）¹⁰，其中a_k （k=0，1，2，…，9，10）都是常数，则a₁+2a₂+3a₃+…+9a₉+10a₁₀=    ．

Answer 1

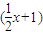【答案】分析：首先将¹⁰变形为（）¹⁰[1+（x+1）]¹⁰，再利用二项式定理展开可得¹⁰=（）¹⁰+（）¹⁰C₁₀¹（1+x）¹+（）¹⁰C₁₀²（1+x）²+…+（）¹⁰C₁₀¹⁰（1+x）¹⁰；结合题意，可得a₁=（）¹⁰C₁₀¹，a₂=（）¹⁰C₁₀²，…a₁₀=（）¹⁰C₁₀¹⁰，进而可得a₁+2a₂+3a₃+…+9a₉+10a₁₀=（）¹⁰C₁₀¹+（）¹⁰C₁₀²+…（）¹⁰C₁₀¹⁰=（）¹⁰[C₁₀¹+2C₁₀²+…+10C₁₀¹⁰]，由二项式系数的性质，可得a₁+2a₂+3a₃+…+9a₉+10a₁₀=（）¹⁰×10×[C₉+C₉¹+…+C₉⁹]=（）¹⁰×10×2⁹，计算可得答案．
解答：解：¹⁰=（）¹⁰[1+（x+1）]¹⁰=（）¹⁰+（）¹⁰C₁₀¹（1+x）¹+（）¹⁰C₁₀²（1+x）²+…+（）¹⁰C₁₀¹⁰（1+x）¹⁰；
根据题意，¹⁰=a+a₁（x+1）+a₂（x+1）²+…+a₉（x+1）⁹+a₁₀（x+1）¹⁰，
则a=（）¹⁰，a₁=（）¹⁰C₁₀¹，a₂=（）¹⁰C₁₀²，…a₁₀=（）¹⁰C₁₀¹⁰，
则a₁+2a₂+3a₃+…+9a₉+10a₁₀=（）¹⁰C₁₀¹+2（）¹⁰C₁₀²+…+10（）¹⁰C₁₀¹⁰，
=（）¹⁰[C₁₀¹+2C₁₀²+…+10C₁₀¹⁰]，
又由mC_n^m=nC_n-1^m-1，则C₁₀¹=10C₉，2C₁₀²=10C₉¹，…，10C₁₀¹⁰=10C₉⁹，
即a₁+2a₂+3a₃+…+9a₉+10a₁₀=（）¹⁰×10×[C₉+C₉¹+…+C₉⁹]=（）¹⁰×10×2⁹=5；
故答案为5．
点评：本题考查二项式定理的运用，解题的关键要灵活运用二项式系数的性质．