
【题目】已知数列![]() 的首项
的首项![]() ,且
,且![]() ,
,![]() .
.
(1)证明: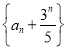 是等比数列;
是等比数列;
(2)若![]() ,
,![]() 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在,请说明理由;
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在,请说明理由;
(3)若![]() 是递减数列,求
是递减数列,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题甲是命题乙的充分非必要条件,命题丙是命题乙的必要非充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( )
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的极值点为
的极值点为![]() ,当
,当![]() 变化时,点(
变化时,点(![]() ,
,![]() )构成曲线M.证明:任意过原点的直线
)构成曲线M.证明:任意过原点的直线![]() ,与曲线M均仅有一个公共点.
,与曲线M均仅有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意![]() 都有
都有![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() ,给出如下命题:
,给出如下命题:
①![]() ;
;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
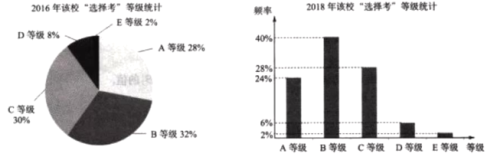
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在研究几何时曾定义欧拉三角形,![]() 的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为
的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为![]() 的欧拉三角形.如图,
的欧拉三角形.如图,![]() 是
是![]() 的欧拉三角形(H为
的欧拉三角形(H为![]() 的垂心).已知
的垂心).已知![]() ,
,![]() ,
,![]() ,若在
,若在![]() 内部随机选取一点,则此点取自阴影部分的概率为________.
内部随机选取一点,则此点取自阴影部分的概率为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com