(I)证明:由a
n+a
n+1=2
n,得a
n+1=2
n-a
n,所以
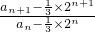
=
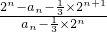
=-1
又因为a
1-

=

,所以数列{a
n-

×2
n}是首项为

,公比为-1的等比数列.
所以a
n-

×2
n=

×(-1)
n-1,即a
n=

[2
n-(-1)
n],所以b
n=2
n-(-1)
n. (5分)
(II)解:假设在数列{b
n}中,存在连续三项b
k-1,b
k,b
k+1(k∈N
*,k≥2)成等差数列,则b
k-1+b
k+1=2b
k,
即[2
k-1-(-1)
k-1]+[2
k+1-(-1)
k+1]=2[2
k-(-1)
k],即2
k-1=4(-1)
k-1.
①若k为偶数,则2
k-1>0,4(-1)
k-1=-4<0,所以,不存在偶数k,使得b
k-1,b
k,b
k+1成等差数列.(7分)
②若k为奇数,则当k≥3时,2
k-1≥4,而4(-1)
k-1=4,所以,当且仅当k=3时,b
k-1,b
k,b
k+1成等差数列.
综上所述,在数列{b
n}中,有且仅有连续三项b
2,b
3,b
4成等差数列.(9分)
(III)证明:要使b
1,b
r,b
s成等差数列,只需b
1+b
s=2b
r,
即3+2
s-(-1)
s=2[2
r-(-1)
r],即2
s-2
r+1=(-1)
s-2(-1)
r-3,(﹡) (10分)
①若s=r+1,在(﹡)式中,左端2
s-2
r+1=0,
右端(-1)
s-2(-1)
r-3=(-1)
s+2(-1)
s-3=3(-1)
s-3,
要使(﹡)式成立,当且仅当s为偶数时.又s>r>1,且s,r为正整数,
所以当s为不小于4的正偶数,且s=r+1时,b
1,b
r,b
s成等差数列.(12分)
②若s≥r+2时,在(﹡)式中,左端2
s-2
r+1≥2
r+2-2
r+1=2
r+1,
由(II)可知,r≥3,所以r+1≥4,所以左端2
s-2
r+1≥16(当且仅当s为偶数、r为奇数时取“=”);右端(-1)
s-2(-1)
s-3≤0.所以当s≥r+2时,b
1,b
r,b
s不成等差数列.
综上所述,存在不小于4的正偶数s,且s=r+1,使得b
1,b
r,b
s成等差数列. (14分)
分析:(I)由a
n+a
n+1=2
n,得a
n+1=2
n-a
n,从而可证
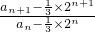
=-1,即可证得数列
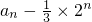
是等比数列,并可求数列{b
n}的通项公式;
(II)解:假设在数列{b
n}中,存在连续三项b
k-1,b
k,b
k+1(k∈N
*,k≥2)成等差数列,则b
k-1+b
k+1=2b
k,即2
k-1=4(-1)
k-1.分类讨论,可得在数列{b
n}中,有且仅有连续三项b
2,b
3,b
4成等差数列;
(III)证明:要使b
1,b
r,b
s成等差数列,只需b
1+b
s=2b
r,即2
s-2
r+1=(-1)
s-2(-1)
r-3,(﹡),分类讨论,可知存在不小于4的正偶数s,且s=r+1,使得b
1,b
r,b
s成等差数列.
点评:本题主要考查等比数列的判定和等差数列的应用,考查函数与方程,分类讨论思想,考查推理论证能力.

 .
.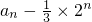 是等比数列,并求数列{bn}的通项公式;
是等比数列,并求数列{bn}的通项公式;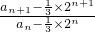 =
=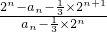 =-1
=-1 =
= ,所以数列{an-
,所以数列{an- ×2n}是首项为
×2n}是首项为 ,公比为-1的等比数列.
,公比为-1的等比数列. ×2n=
×2n= ×(-1)n-1,即an=
×(-1)n-1,即an= [2n-(-1)n],所以bn=2n-(-1)n. (5分)
[2n-(-1)n],所以bn=2n-(-1)n. (5分)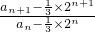 =-1,即可证得数列
=-1,即可证得数列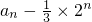 是等比数列,并可求数列{bn}的通项公式;
是等比数列,并可求数列{bn}的通项公式;

 名校课堂系列答案
名校课堂系列答案 .
. 是等比数列,并求数列{bn}的通项公式;
是等比数列,并求数列{bn}的通项公式; .
. 是等比数列,并求数列{bn}的通项公式;
是等比数列,并求数列{bn}的通项公式;