
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,b=2 ![]() ,B=
,B= ![]() .
.
(1)若a=2,求角C;
(2)若D为AC的中点,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:在△ABC中,由正弦定理可得: ![]() ,
,
∴sinA= ![]() =
= ![]() =
= ![]() ,
,
又a<b,∴A为锐角,A= ![]() ,
,
∴C=π﹣A﹣B= ![]() .
.
(2)解:在△ABC中,由余弦定理可得: ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() ,化为:a2+c2+ac=12.
,化为:a2+c2+ac=12.
在△ABD与△BCD中,由余弦定理可得:cos∠ADB+cos∠BDC= ![]() +
+ ![]() =0,
=0,
化为:a2+c2=10.
与a2+c2+ac=12联立解得:ac=2,
∴S△ABC= ![]() =
= ![]()
【解析】(1)在△ABC中,由正弦定理可得: ![]() ,可得sinA=
,可得sinA= ![]() ,又a<b,可得A为锐角,可得C=π﹣A﹣B.(2)在△ABC中,由余弦定理可得:
,又a<b,可得A为锐角,可得C=π﹣A﹣B.(2)在△ABC中,由余弦定理可得: ![]() =
= ![]() =﹣
=﹣ ![]() ,化为:a2+c2+ac=12.在△ABD与△BCD中,由余弦定理可得:cos∠ADB+cos∠BDC=0,化为:a2+c2=10.联立解出即可得出.
,化为:a2+c2+ac=12.在△ABD与△BCD中,由余弦定理可得:cos∠ADB+cos∠BDC=0,化为:a2+c2=10.联立解出即可得出.
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ),还要掌握余弦定理的定义(余弦定理:
),还要掌握余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=(kx+4)lnx﹣x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
A.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() )
)
B.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() ]
]
C.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1]
﹣1]
D.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1)
﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项为正数的数列{an}的前n项和为Sn , 且满足:Sn= ![]() an2+
an2+ ![]() an+
an+ ![]() (n∈N*)
(n∈N*)
(1)求an
(2)设数列{ ![]() }的前n项和为Tn , 证明:对一切正整数n,都有Tn<
}的前n项和为Tn , 证明:对一切正整数n,都有Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示. 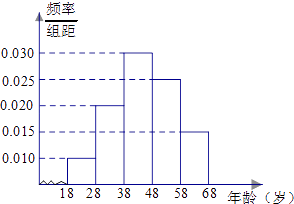
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 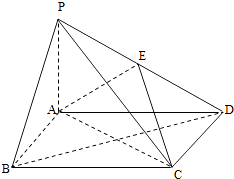
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() ,
,![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,甲向如图1所示的平面区域内随机掷点、乙向如图2所示的平面区域内随机掷点,假设点落在区域内任意一点的可能性相同.已知图1中小圆的半径是大圆半径的二分之一,图2中小正方形的顶点为大正方形各边的中点.
(1)甲、乙各掷点一次,求至少有一人掷点落在阴影区域的概率;
(2)甲、乙各掷点两次,记点落在阴影区域的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

图1图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z1=m+ni(m,n∈R),z=x+yi(x,y∈R),z2=2+4i且 ![]() .
.
(1)若复数z1对应的点M(m,n)在曲线 ![]() 上运动,求复数z所对应的点P(x,y)的轨迹方程;
上运动,求复数z所对应的点P(x,y)的轨迹方程;
(2)将(1)中的轨迹上每一点按向量 ![]() 方向平移
方向平移 ![]() 个单位,得到新的轨迹C,求C的轨迹方程;
个单位,得到新的轨迹C,求C的轨迹方程;
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com