
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{10}}{2}$ |
分析 由已知得PF1⊥PF2,由tan∠PF1F2=$\frac{1}{3}$,得$\frac{P{F}_{2}}{P{F}_{1}}$=$\frac{1}{3}$,设PF2=x,则PF1=3x,F1F2=2c=$\sqrt{10}x$,由双曲线定义得2a=PF1-PF2=3x-x=2x,由此能求出该双曲线的离心率.
解答 解: 如图,∵点P在以点F1,F2分别为左、右焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,且满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,
如图,∵点P在以点F1,F2分别为左、右焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,且满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,
∴PF1⊥PF2,∵tan∠PF1F2=$\frac{1}{3}$,∴$\frac{P{F}_{2}}{P{F}_{1}}$=$\frac{1}{3}$,
设PF2=x,则PF1=3x,
∴F1F2=2c=$\sqrt{P{{F}_{1}}^{2}+P{{F}_{2}}^{2}}$=$\sqrt{9{x}^{2}+{x}^{2}}$=$\sqrt{10}x$,
由双曲线定义得2a=PF1-PF2=3x-x=2x,
∴该双曲线的离心率e=$\frac{c}{a}$=$\frac{2c}{2a}$=$\frac{\sqrt{10}}{2}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用勾股定理和双曲线的定义,考查运算能力,属于中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
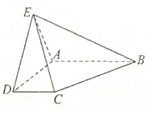 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com