（2007北京四中模拟一）在△ABC中，A点的坐标为（3，0），BC边长为2，且BC在y轴上的区间[-3，3]上滑动．
（1）求△ABC外心的轨迹方程；
（2）设直线l∶y＝3x＋b与（1）的轨迹交于E，F两点，原点到直线l的距离为d，求
的最大值．并求出此时b的值．
名校课堂系列答案科目：高中数学 来源： 题型：022
(2007
北京宣武模拟)一次文艺演出中，需要给舞台上方安排一排完全相同的彩灯共15只，以不同的点亮方式增加舞台效果，设计要求如下：恰好有6只是关的，且相邻的灯不能同时被关掉，两端的灯必须点亮，那么不同的点亮方式的种数是______(用数字作答)．查看答案和解析>>
科目：高中数学 来源： 题型：013
(2007
北京海淀模拟)动点P为椭圆
(a＞b＞0)上异于椭圆顶点(±a，0)的一点，
、
为椭圆的两个焦点，动圆C与线段
、
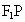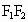的延长线及线段
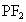相切，则圆心C的轨迹为除去坐标轴上的点的
[
]|
A ．一条直线 |
B ．双曲线的右支 |
|
C ．抛物线 |
D ．椭圆 |
查看答案和解析>>
科目：高中数学 来源： 题型：044
(2007
北京海淀模拟)某公司有10万元资金用于投资，如果投资甲项目，根据市场分析知道：一年后可能获利10％，可能损失10％，可能不赔不赚，这三种情况发生的概率分别为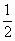
，
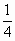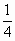，；如果投资乙项目，一年后可能获利20％，也可能损失20％，这两种情况发生的概率分别为α和β(α＋β=1)．
(1)
如果把10万元投资甲项目，用ξ表示投资收益(收益=回收资金－投资资金)，求ξ的概率分布及Eξ；(2)
若把10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益，求α的取值范围．查看答案和解析>>
科目：高中数学 来源： 题型：044
(2007
北京崇文模拟)已知盒子里有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，标号为4的球3个．(1)
若从盒子里一次任取3个球，假设取出每个球的可能性都相同，求取出的三个球中标号为1，2，4的球各一个的概率；(2)
若第一次从盒子里任取1个球，放回后，第二次再任取1个球，假设取出每个球的可能性都相同，记第一次与第二次取出球的标号之和为ξ，求随机变量ξ的数学期望．查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．，
），则C点坐标为（0，
②由①②消去
．∵
，∴
．故所求的△ABC外心的轨迹方程为：
代入
．由
及
，得
．所以方程①在区间
，2
有两个实根．设
，则方程③在
得
∴
，
∵
．
，即
．
