
命题“?x∈R,使x2+ax+4<0”的否定是 .
科目:高中数学 来源: 题型:填空题
有下列命题中假命题的序号是
①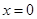 是函数
是函数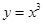 的极值点;
的极值点;
②三次函数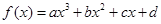 有极值点的充要条件是
有极值点的充要条件是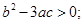
③奇函数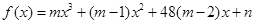 在区间
在区间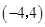 上单调递减.
上单调递减.
④若双曲线的渐近线方程为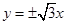 ,则其离心率为2.
,则其离心率为2.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
以下五个命题: ①标准差越小,则反映样本数据的离散程度越大; ②两个随机变量相关性越强,则相关系数越接近1; ③在回归直线方程 中,当解释变量
中,当解释变量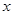 每增加1个单位时,则预报变量
每增加1个单位时,则预报变量 减少0.4个单位; ④对分类变量X与Y来说,它们的随机变量
减少0.4个单位; ④对分类变量X与Y来说,它们的随机变量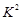 的观测值
的观测值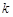 越小,“X与Y有关系”的把握程度越大; ⑤在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
越小,“X与Y有关系”的把握程度越大; ⑤在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
其中正确的命题是: (填上你认为正确的命题序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面直角坐标系中,定义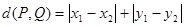 为两点
为两点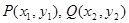 ,之间的“折线距离”.在这个定义下,给出下列命题:
,之间的“折线距离”.在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个正方形;
②到原点的“折线距离”等于1的点的集合是一个圆;
③到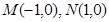 两点的“折线距离”之和为4的点的集合是面积为6的六边形;
两点的“折线距离”之和为4的点的集合是面积为6的六边形;
④到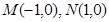 两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
其中正确的命题是___________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知下列结论:
①已知 为实数,则“
为实数,则“ ”是“
”是“ 成等比数列”的充要条件;
成等比数列”的充要条件;
②满足条件 的△ABC的个数为2;
的△ABC的个数为2;
③若两向量 的夹角为钝角,则实数
的夹角为钝角,则实数 的取值范围
的取值范围
为 ;
;
④若 为三角形中的最小内角,则函数
为三角形中的最小内角,则函数 的值域是
的值域是 ;
;
⑤某厂去年12月份产值是同年一月份产值的m倍,则该厂去年的月平均增长率
为 ;
;
则其中正确结论的序号是__________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com