
分析 (1)对x分类讨论,利用微积分基本定理即可得出.
(2)利用复数的运算法则、纯虚数的定义即可得出.
解答 解:(1)${∫}_{-2}^{1}$|x2-2|dx=${∫}_{-2}^{-\sqrt{2}}({x}^{2}-2)dx$+${∫}_{-\sqrt{2}}^{1}$(2-x2)dx=$(\frac{{x}^{3}}{3}-2x){|}_{-2}^{-\sqrt{2}}$+$(2x-\frac{{x}^{3}}{3}){|}_{-\sqrt{2}}^{1}$=$\frac{8}{3}\sqrt{2}$+$\frac{1}{3}$.
(2)∵$\frac{{z}_{1}}{{z}_{2}}$=$\frac{a+2i}{3-4i}$=$\frac{(a+2i)(3+4i)}{(3-4i)(3+4i)}$=$\frac{3a-8}{25}$+$\frac{(4a+6)}{25}$i为纯虚数,
∴$\frac{3a-8}{25}$=0,$\frac{(4a+6)}{25}$≠0,
解得a=$\frac{8}{3}$.
点评 本题考查了微积分基本定理、复数的运算法则、纯虚数的定义,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,11) | B. | (11,5) | C. | (7,5) | D. | (5,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
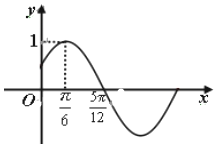 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com