
数列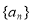 的前n项和记为
的前n项和记为 点
点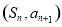 在直线
在直线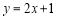 上,
上,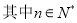 .(1)若数列
.(1)若数列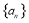 是等比数列,求实数
是等比数列,求实数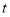 的值;
的值;
(2)设各项均不为0的数列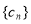 中,所有满足
中,所有满足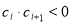 的整数
的整数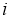 的个数称为这个数列
的个数称为这个数列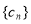 的“积异号数”,令
的“积异号数”,令 (
(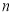
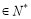 ),在(1)的条件下,求数列
),在(1)的条件下,求数列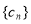 的“积异号数”
的“积异号数”
(1)1 (2)1
【解析】
试题分析:(1)根据数列的第n项与前n项和的关系可得n≥2时,有 ,化简得an+1=3an (n≥2),要使n≥1时{an}是等比数列,只需
,化简得an+1=3an (n≥2),要使n≥1时{an}是等比数列,只需 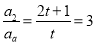 ,从而得出t的值.
,从而得出t的值.
(2)由条件求得cn=1? 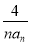 =
=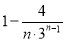 ,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2=
,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2=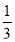 >0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.
>0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.
(1)由题意,当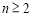 时,有
时,有
两式相减,得 , 3分
, 3分
所以,当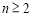 时
时 是等比数列,要使
是等比数列,要使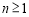 时
时 是等比数列,则只需
是等比数列,则只需
从而得出 5分
5分
(2)由(1)得,等比数列 的首项为
的首项为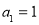 ,公比
,公比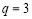 ,∴
,∴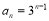
∴
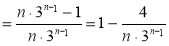 7分
7分
∵ ,
, ,∴
,∴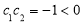
∵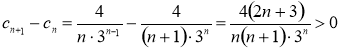 ,
,
∴数列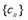 递增. 10分
递增. 10分
由 ,得当
,得当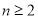 时,
时,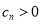 .
.
∴数列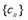 的“积异号数”为1. 12分
的“积异号数”为1. 12分
考点:1.数列与函数的综合;2.等比关系的确定;3.数列的求和.


科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
正方形 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,将此正
,将此正
方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥 的体积是( )
的体积是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知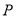 、
、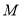 、
、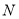 是单位圆上互不相同的三个点,且满足
是单位圆上互不相同的三个点,且满足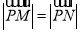 ,则
,则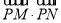
的最小值是( )
A. B.
B.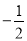 C.
C.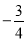 D.
D.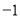
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考理科数学试卷(解析版) 题型:填空题
已知集合M={ },若对于任意
},若对于任意 ,存在
,存在 ,使得
,使得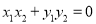 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ };
};
②M={ };
};
③M={ };
};
④M={ }.
}.
其中是“垂直对点集”的序号是 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com