
【题目】解答题。
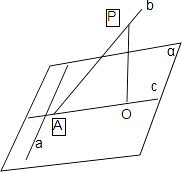
(1)如图,证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明) 
【答案】
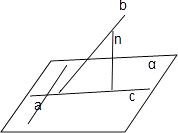
(1)证明:证法一:如图,过直线b上任一点作平面α的垂线n,设直线a,b,c,n对应的方向向量分别是 ![]() ,则
,则 ![]() 共面,
共面,
根据平面向量基本定理,存在实数λ,μ使得 ![]() ,
,
则 ![]() =
= ![]()
因为a⊥b,所以 ![]() ,
,
又因为aα,n⊥α,
所以 ![]() ,
,
故 ![]() ,从而a⊥c
,从而a⊥c
证法二
如图,记c∩b=A,P为直线b上异于点A的任意一点,过P做PO⊥π,垂足为O,则O∈c,
∵PO⊥π,aπ,
∴直线PO⊥a,
又a⊥b,b平面PAO,PO∩b=P,
∴a⊥平面PAO,
又c平面PAO,
∴a⊥c
(2)证明:逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b,
逆命题为真命题
【解析】(1)证法一:做出辅助线,在直线上构造对应的方向向量,要证两条直线垂直,只要证明两条直线对应的向量的数量积等于0,根据向量的运算法则得到结果.证法二:做出辅助线,根据线面垂直的性质,得到线线垂直,根据线面垂直的判定定理,得到线面垂直,再根据性质得到结论.(2)把所给的命题的题设和结论交换位置,得到原命题的逆命题,判断出你命题的正确性.


科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市疾病控制中心今日对我校高二学生进行了某项健康调查,调查的方法是采取分层抽样的方法抽取样本.我校高二学生共有2000人,抽取了一人200人的样本,样本中男生103人,请问我校共有女生( )
A.970
B.1030
C.997
D.206
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对甲乙两个车间各10名工人生产的合格产品的统计结果的茎叶图.设甲、乙的中位数分别为x甲、x乙 , 甲、乙的方差分别为s甲2、s乙2 , 则( ) 
A.x甲<x乙 , s甲2<s乙2
B.x甲>x乙 , s甲2>s乙2
C.x甲>x乙 , s甲2<s乙2
D.x甲<x乙 , s甲2>s乙2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,E为BC上的动点. 
(1)当E为BC的中点时,求证:PE⊥DE;
(2)设PA=1,在线段BC上存在这样的点E,使得二面角P﹣ED﹣A的平面角大小为 ![]() .试确定点E的位置.
.试确定点E的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A为以原点O为圆心的单位圆O与x正半轴的交点,在圆心角为 ![]() 的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ.
的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ. 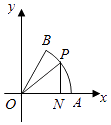
(1)设△PON的面积为y,使y取得最大值时的点P记为E,点N记为F,求此时 ![]() 的值;
的值;
(2)求k=a| ![]() ||
|| ![]() |+
|+ ![]() (a∈R,E 是在(1)条件下的点 E)的值域.
(a∈R,E 是在(1)条件下的点 E)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c,其对称轴为y轴(其中b,c为常数) (Ⅰ)求实数b的值;
(Ⅱ)记函数g(x)=f(x)﹣2,若函数g(x)有两个不同的零点,求实数c的取值范围;
(Ⅲ)求证:不等式f(c2+1)>f(c)对任意c∈R成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,PA是四棱锥的高,PB与DC所成角为45°,F是PB的中点,E是BC上的动点.
(Ⅰ)证明:PE⊥AF;
(Ⅱ)若BC=2BE=2 ![]() AB,求直线AP与平面PDE所成角的大小..
AB,求直线AP与平面PDE所成角的大小..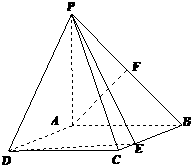
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com