
【题目】某公司决定投人资金进行产品研发以提高产品售价.已知每件产品的制造成本为![]() 元,若投人的总的研发成本
元,若投人的总的研发成本![]() (万元)与每件产品的销售单价
(万元)与每件产品的销售单价![]() (元)的关系如下表:
(元)的关系如下表:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)市场部发现,销售单价![]() (元)与销量
(元)与销量![]() (件)存在以下关系:
(件)存在以下关系:![]() ,
,![]() .根据(1)中结果预测,当
.根据(1)中结果预测,当![]() 为何值时,可获得最高的利润?
为何值时,可获得最高的利润?
附: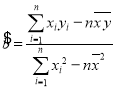 ,
,![]() .
.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() 都有
都有![]() 成立,试求
成立,试求![]() 的取值范围;
的取值范围;
(3)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
B.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
C.若随机变量![]() 服从二项分布:
服从二项分布:![]() ,则
,则![]() ;
;
D.已知直线![]() 经过点
经过点![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新的劳动合同法出台后,某公司实行了年薪制工资结构改革.该公司从2008年起,每人的工资由三个项目构成,并按下表规定实施:
项目 | 金额[元/(人年)] | 性质与计算方法 |
基础工资 | 2007年基础工资为20000元 | 考虑到物价因素,决定从2008年 起每年递增10%(与工龄无关) |
房屋补贴 | 800 | 按职工到公司年限计算,每年递增800元 |
医疗费 | 3200 | 固定不变 |
如果该公司今年有5位职工,计划从明年起每年新招5名职工.
(1)若今年算第一年,将第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)若公司每年发给职工工资总额中,房屋补贴和医疗费的总和总不会超过基础工资总额的p%,求p的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=cos(asinx)﹣sin(bcosx)没有零点,则a2+b2的取值范围是( )
A.[0,1)B.[0,π2)C.![]() D.[0,π)
D.[0,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为
的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为![]() ,且
,且![]() .
.

(1)求椭圆C的方程;
(2)过椭圆C的左焦点![]() 的直线
的直线![]() 交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线
交椭圆于M、N两点,且该椭圆上存在点P,使得四边形MONP(图形上字母按此顺序排列)恰好为平行四边形,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com