考点:数列与函数的综合
专题:等差数列与等比数列
分析:(1)利用x+y=2且x≠y,通过二次函数的值域,以及不等式的最值,比较
1,xy,的大小,即可得到序数列.
(2)通过证明充分性和必要性,两个方面证明有穷数列{a
n}的序数列{p
n}为等差数列的充要条件是有穷数列{a
n}为单调数列.
(3)利用数列的表达式,说明当n=1时,b
2>b
1,当n≥2时,b
n+1<b
n,推出b
2>b
3>b
1>b
4>…>b
n,得到数列{b
n}的序数列为2,3,1,4,…,n.然后利用数列{c
n}结合二次函数的性质,推出4<t<5.
解答:
解:(1)因为x+y=2且x≠y,
所以xy=x(2-x)=-(x-1)
2+1<1,…..2’.
==(x-1)2+1>1…..4’
故数列
1,xy,的序数列3,1,2;…..5’
(2)充分性:因为数列{a
n}是单调数列时,a
1>a
2>…>a
n或a
1<a
2<…<a
n,
所以其序数列为1,2,…,n-1,n或n,n-1,…,2,1均为等差数列;…..8’
必要性:当数列{a
n}的序数列为等差数列时,其序数列必为1,2,…,n-1,n或n,n-1,…,2,1,
所以有a
1>a
2>…>a
n或a
1<a
2<…<a
n,
所以数列{a
n}为单调数列;…..11’
(3)因为
bn+1-bn=()n•,…..13’
当n=1时,易得b
2>b
1,当n≥2时,b
n+1<b
n,
又因
b1=,
b3=3•()3,
b4=4•()4,b
4<b
1<b
3,
即b
2>b
3>b
1>b
4>…>b
n,
故数列{b
n}的序数列为2,3,1,4,…,n,…..16’
所以对于数列{c
n}有c
2>c
3>c
1>c
4>…>c
n,c
n=-n
2+tn(n∈N
*),
可得
2<<,解得:4<t<5…..18’
点评:本题考查数列与函数相结合的综合应用,二次函数的最值以及性质,不等式的应用,考查分析问题解决问题以及转化思想的应用.



 如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点B(-
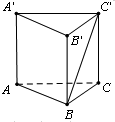 如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=
如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=