
分析 求导,得f′(x)=ax2+2ax-3a=a(x+3)(x-1),要使函数f(x)的图象经过四个象限,则f(-3)f(1)<0,再进一步计算即可.
解答 解:∵f(x)=$\frac{1}{3}$ax3+ax2-3ax+1
∴f′(x)=ax2+2ax-3a=a(x-1)(x+3),
令f′(x)=0,
解的x=1或x=-3,
要使函数f(x)的图象经过四个象限,则f(-3)f(1)<0,
∵f(-3)=$\frac{1}{3}$a(-3)3+a(-3)2-3a(-3)+1=9a+1,
f(1)=$\frac{1}{3}$a+a-3a+1=1-$\frac{5}{3}$a,
∴(9a+1)(1-$\frac{5}{3}$a)<0,
即(a+$\frac{1}{9}$)(a-$\frac{3}{5}$)>0,
解的a<-$\frac{1}{9}$,或a>$\frac{3}{5}$
故答案为:(-∞,-$\frac{1}{9}$)∪($\frac{3}{5}$,+∞).
点评 本题考查函数与导数的应用,利用导数判断函数的单调性,函数值的变化从而确定其性质.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
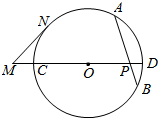 如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.
如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
在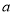 和
和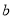 两数之间插入5个数,使他们与
两数之间插入5个数,使他们与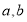 组成等差数列,则该数列的公差为( )
组成等差数列,则该数列的公差为( )
A.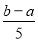 B.
B.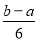 C.
C.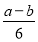 D.
D.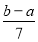
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<0<g(a) | B. | g(a)<0<f(b) | C. | f(b)<g(a)<0 | D. | 0<g(a)<f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
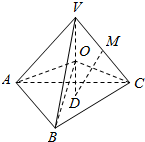 如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.
如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com