
设A、B分别为双曲线![]() =1(a>0,b>0)的左、右两个顶点,P为双曲线上一点, |AB|=|BP|=4,
=1(a>0,b>0)的左、右两个顶点,P为双曲线上一点, |AB|=|BP|=4,
∠PAB=30°.
(1)求双曲线的方程;
(2)设M为(1)中双曲线上任一动点,过B点作直线l1,使得l1⊥BM,过A点作直线l2,使得l2⊥AM,l1、l2相交于点N,求点N的轨迹方程.
解:(1)∵|AB|=4,
∴2a=4,即a=2.

过P点作PC⊥x轴,C为垂足.
在△ABP中,
∵|AB|=|BP|=4,
∠PAB=30°,
∴∠PBC=2∠PAB=60°.
∴|PC|=|PB|·sin60°=2![]() .
.
∴P(4,2![]() ).
).
又∵点P为双曲线上任意一点,则![]() =1.
=1.
∴b2=4.
故所求双曲线的方程为![]() -
-![]() =1.
=1.
(2)设M(x0,y0)、N(x,y).∵A(-2,0)、B(2,0),
NB⊥MB,NA⊥MA,
∴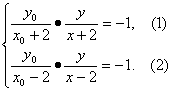
由(1)×(2)得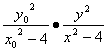 =1. (3)
=1. (3)
又∵M(x0,y0)在双曲线上,
∴![]() =1.∴
=1.∴ =1.代入(3)中,
=1.代入(3)中,
得![]() =1,即x2-y2=4.
=1,即x2-y2=4.
经检验点(-2,0)、(2,0)不符合题意.
故N点轨迹方程为x2-y2=4(x≠±2).


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| ||
| 3 |
| OM |
| ON |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
设A、B分别为双曲线![]() =1(a>0,b>0)的左、右两个顶点,P为双曲线上一点, |AB|=|BP|=4,∠PAB=30°.
=1(a>0,b>0)的左、右两个顶点,P为双曲线上一点, |AB|=|BP|=4,∠PAB=30°.
(1)求双曲线的方程;
(2)设M为(1)中双曲线上任一动点,过B点作直线l1,使得l1⊥BM,过A点作直线l2,使得l2⊥AM,l1、l2相交于点N,求点N的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| ||
| 3 |
| OM |
| ON |
| OD |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省郴州市安仁一中高三(上)月考数学试卷(文科)(解析版) 题型:解答题
 的左右顶点,双曲线的实轴长为
的左右顶点,双曲线的实轴长为 ,焦点到渐近线的距离为
,焦点到渐近线的距离为 .
. 与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使
与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使 ,求t的值及点D的坐标.
,求t的值及点D的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com