
【题目】如图1,在平面四边形ABCD中,![]() ,
,![]() ,
,![]() 且
且![]() .将
.将![]() 沿BD折成如图2所示的三棱锥
沿BD折成如图2所示的三棱锥![]() ,使
,使![]() .
.

(1)证明:![]() ;
;
(2)求三棱锥![]() 与三棱锥
与三棱锥![]() 的高的比.
的高的比.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
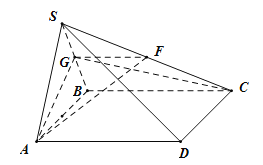
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
![]() 函数
函数![]() 的最大值为1;
的最大值为1;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”;
”;
![]() 若
若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
![]() “
“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蹴鞠起源于春秋战国,是现代足球的前身.到了唐代,制作的蹴鞠已接近于现代足球,做法是:用八片鞣制好的尖皮缝制成“圆形”的球壳,在球壳内放一个动物膀胱,“嘘气闭而吹之”,成为充气的球.如图所示,将八个全等的正三角形缝制成一个空间几何体,在几何体内放一个气球,往气球内充气使几何体膨胀,当几何体膨胀成球体(顶点位置不变)且恰好是原几何体外接球时,测得球的体积是![]() ,则正三角形的边长为( )
,则正三角形的边长为( )
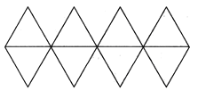
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
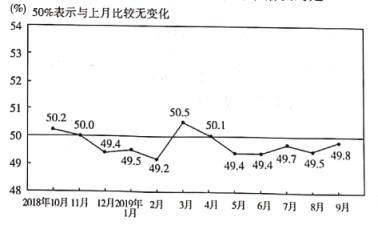
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com