考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)建立坐标系,利用向量法证明AE⊥平面BCF;
(2)由题意,F到A1C1的距离即为所求.
解答:
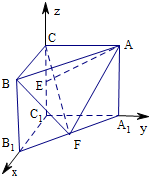
(1)证明:建立以C
1为坐标原点的空间坐标系如图,
∵AC=BC=AA
1=2,E,F分别是CC
1,A
1B
1的中点.
∴A(0,2,2),B(2,0,2),E(0,0,1),A
1(0,2,0),F(1,1,0),B
1(2,0,0),C(0,0,2)
则
=(0,-2,-1),
=(-2,0,0),
=(1,1,-2),
则
•
=0,
•
=-2+2=0,
则
⊥
,
⊥
,
即AE⊥BC,AE⊥CF,BC∩CF=C,
∴AE⊥平面BCF;
(2)解:取AB的中点O,连结CO,FO,
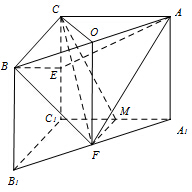
∵CB=CA,
∴CO⊥AB
∴平面ABC⊥平面BB
1A
1A,
∴CO⊥平面ABF,
而CE∥平面BB
1A
1A,
∴E到平面ABF的距离就是CO的长,
CO=AB=,
∴S
△ABF=
AB•OF=2
,
∴
VE-ABF=?CO?S△ABF=,
又Rt△ECB和Rt△ECA中,易知EB=EA=
,
又AB=2
,
故EO=
=
,
∴S
△ABE=
EO•AB=
设F到平面ABE的距离为d,
由V
F-ABE=V
E-ABF,得
S
△ABEd=
,解得d=
.
点评:本题主要考查空间直线和平面垂直的判断,考查F到平面ABE的距离,建立坐标系利用向量法是解决本题的关键.

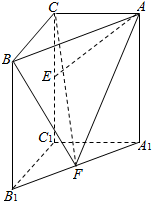 如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点. (1)证明:建立以C1为坐标原点的空间坐标系如图,
(1)证明:建立以C1为坐标原点的空间坐标系如图,

