
 ,在点(1,f(1))处的切线斜率为
,在点(1,f(1))处的切线斜率为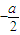 ,且a>2c>b.
,且a>2c>b.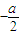 ,可知
,可知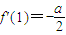 ,得到a、b、c的等量关系,然后利用不等式中的放缩法可判定a与b的符号;
,得到a、b、c的等量关系,然后利用不等式中的放缩法可判定a与b的符号;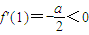 且f'(2)=a-c>0则f(x)在区间(1,2)内至少有一个极值点,当c>0,f'(1)=c>0且
且f'(2)=a-c>0则f(x)在区间(1,2)内至少有一个极值点,当c>0,f'(1)=c>0且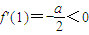 ,则f(x)在区间(0,1)内至少有一个极值点,从而证得结论;
,则f(x)在区间(0,1)内至少有一个极值点,从而证得结论;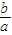 的取值范围,根据题意可知m,n为f'(x)=0的两根,将n-m用
的取值范围,根据题意可知m,n为f'(x)=0的两根,将n-m用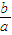 表示,然后根据
表示,然后根据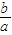 的取值范围可求出n-m的取值范围.
的取值范围可求出n-m的取值范围.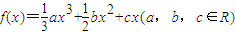 ,
,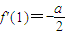
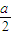 即3a+2b+2c=0①(1分)
即3a+2b+2c=0①(1分) 且f'(2)=a-c>0
且f'(2)=a-c>0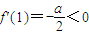
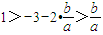
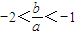 ②(9分)
②(9分)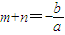 ③
③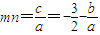 ④(10分)
④(10分)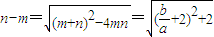
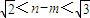 ,
,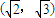 (12分)
(12分)

科目:高中数学 来源: 题型:
| A、y=4x | ||
| B、y=4x-8 | ||
| C、y=2x+2 | ||
D、y=-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a>0,a∈R,函数![]()
(I)设曲线y=![]() 在点(1,f(1))处的切线为直线l,若直线l与圆(x+1)2+y2=1相切,求实数a的值;
在点(1,f(1))处的切线为直线l,若直线l与圆(x+1)2+y2=1相切,求实数a的值;
(II)求函数![]() 的单调区间;
的单调区间;
(III)求函数![]() 在[0,1]上的最小值.
在[0,1]上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com