
【题目】设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是![]() 和an的等差中项.
和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=-n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
【答案】(1)见解析;(2)当n=2或n=3时,{an·bn}的最大项的值为6.
【解析】试题分析:(1)第(1)问,利用项和公式推理,最后证明数列{an}为等差数列.(2)第(2)问,先计算出an·bn,再利用二次函数求它的最大值.
试题解析:
(1)证明:由已知可得2Sn=![]() +an,且an>0,
+an,且an>0,
当n=1时,2a1=![]() +a1,解得a1=1;
+a1,解得a1=1;
当n≥2时,有2Sn-1=![]() +an-1,
+an-1,
所以2an=2Sn-2Sn-1=![]() -
-![]() +an-an-1,所以
+an-an-1,所以![]() -
-![]() =an+an-1,
=an+an-1,
即(an+an-1)(an-an-1)=an+an-1,
因为an+an-1>0,所以an-an-1=1(n≥2).
故数列{an}是首项为1,公差为1的等差数列.
(2)由(1)可知an=n,设cn=an·bn,则cn=n(-n+5)=-n2+5n=-![]()
因为n∈N*,当n=2或n=3时,{an·bn}的最大项的值为6.


科目:高中数学 来源: 题型:
【题目】某学校![]() 、
、![]() 两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
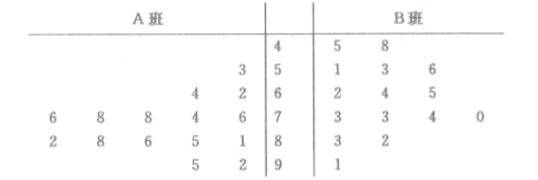
①![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
②![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
③![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
④![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
其中正确结论的编号为( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在30天内每件的销售价![]() (元)与时间
(元)与时间![]() (天)的函数关系如图表示,该商品在30天内日销售量
(天)的函数关系如图表示,该商品在30天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系为函数
(天)之间的关系为函数![]() .
.
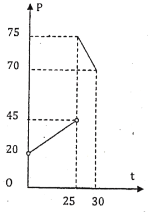
(1)根据提供的图像,写出商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式;
的函数关系式;
(2)若已知![]() ,求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天。(日销售金额=每件的销售价格×日销售量)
,求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天。(日销售金额=每件的销售价格×日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在(-∞,+∞)上有意义,且对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|并且函数f(x+1)的对称中心是(-1,0),若函数g(x)-f(x)=x,则不等式g(2x-x2)+g(x-2)<0的解集是( ).
A.![]() B.
B.![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①命题“x∈R,cosx>0”的否定是“x0∈R,cosx0≤0”;
②若0<a<1,则函数f(x)=x2+ax-3只有一个零点;
③函数y=2![]() sinxcosx在
sinxcosx在![]() 上是单调递减函数;
上是单调递减函数;
④若lga+lgb=lg(a+b),则a+b的最小值为4.
其中真命题的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com