
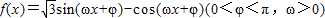 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为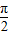 .
.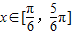 时,求f(x)的取值范围;
时,求f(x)的取值范围;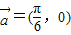 平移后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
平移后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.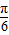 )=0,从而结合题意可求得φ,由其周期可求得ω,从而得到解析式,利用正弦函数的性质可求得x∈[
)=0,从而结合题意可求得φ,由其周期可求得ω,从而得到解析式,利用正弦函数的性质可求得x∈[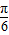 ,
,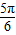 ]时,f(x)的取值范围;
]时,f(x)的取值范围;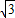 sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-
sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-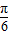 ),
),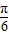 )=sin(ωx+φ-
)=sin(ωx+φ-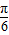 ),
),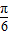 )+cosωxsin(φ-
)+cosωxsin(φ-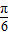 )=sinωxcos(φ-
)=sinωxcos(φ-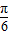 )+cosωxsin(φ-
)+cosωxsin(φ-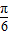 ),
),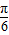 )=0,
)=0,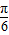 )=0,
)=0,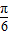 =
=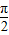 ,
,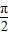 )=2cosωx,
)=2cosωx,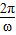 =2•
=2•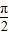 =π,
=π,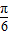 ,
,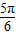 ],
],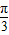 ,
,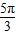 ],
], ],
], -
-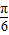 )=2cos[2(
)=2cos[2(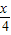 -
-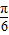 )]=2cos(
)]=2cos(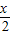 -
-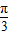 ),
),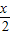 -
-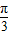 ≤2kπ+π(k∈Z)得:4kπ+
≤2kπ+π(k∈Z)得:4kπ+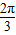 ≤x≤4kπ+
≤x≤4kπ+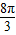 (k∈Z)
(k∈Z)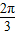 ≤x≤4kπ+
≤x≤4kπ+ ](k∈Z)…(13分)
](k∈Z)…(13分)

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:2013-2014学年浙江省浙北名校联盟高三上学期期中联考理科数学试卷(解析版) 题型:选择题
已知函数 为偶函数,且
为偶函数,且 在
在 上递减,设
上递减,设 ,
, ,
, ,则
,则 的大小关系正确的是( )
的大小关系正确的是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2015届山东省济南市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分10分)已知函数 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数.
(1)求 的值,并确定
的值,并确定 的解析式;
的解析式;
(2)若 且
且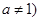 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省、西工大附中高三第五次联考理数 题型:解答题
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com