练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知0<a<1,在函数y= logax  (x≥1)的图象上有A、B、C三点，它们的横坐标分别是t、t+2、t+4；

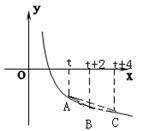    ①、记△ABC的面积为S，求出S=f(t)的表达式；并判断出S== f(t)的单调性；

    ②、求出S=f(t)的最大值。

    解；①、S= f(t) = loga  [] = loga [1- ]；为↘；②、当t=1时，S= f(t)最大值为loga 。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年上虞市质检一理）已知椭圆C1： (0<a<,0<b<2)与椭圆C2：有相同的焦点. 直线L：y=k(x+1)与两个椭圆的四个交点，自上而下顺次记为A、B、C、D.

    (I)求线段BC的长（用k和a表示）;

    (II)是否存在这样的直线L,使线段AB、BC、CD的长按此顺序构成一个等差数列.请说明详细的理由.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西长治二中等四校高三第四次联考理科数学试卷（解析版） 题型：解答题

    以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线的参数方程为 (t为参数，0<a<)，曲线C的极坐标方程为．

    （I）求曲线C的直角坐标方程；

    （II）设直线l与曲线C相交于A、B两点，当a变化时，求|AB|的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西长治二中等四校高三第四次联考文科数学试卷（解析版） 题型：解答题

    以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线的参数方程为 (t为参数，0<a<)，曲线C的极坐标方程为．

    （1）求曲线C的直角坐标方程；

    （2）设直线l与曲线C相交于A、B两点，当a变化时，求|AB|的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0< k <4直线L:kx-2y-2k+8=0和直线M:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则这个四边形面积最小值时k值为                           (    )

    A.2                  B.              C.               D.

     

    查看答案和解析>>

    科目：高中数学 来源：湖北省麻城一中09-10学年高二上学期9月月考（理） 题型：选择题

     已知0< k <4直线L:kx-2y-2k+8=0和直线M:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则这个四边形面积最小值时k值为                           (    )

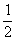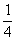    A.2                  B.              C.               D.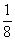

     

    查看答案和解析>>

    同步练习册答案