
【题目】某公司甲、乙两个班组分别试生产同一种规格的产品,已知此种产品的质量指标检测分数不小于70时,该产品为合格品,否则为次品,现随机抽取两个班组生产的此种产品各100件进行检测,其结果如下表:
质量指标检测分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
甲班组生产的产品件数 | 7 | 18 | 40 | 29 | 6 |
乙班组生产的产品件数 | 8 | 12 | 40 | 32 | 8 |
(1)根据表中数据,估计甲、乙两个班组生产该种产品各自的不合格率;
(2)根据以上数据,完成下面的2×2列联表,并判断是否有95%的把握认为该种产品的质量与生产产品的班组有关?
甲班组 | 乙班组 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(3)若按合格与不合格比例,从甲班组生产的产品中抽取4件产品,从乙班组生产的产品中抽取5件产品,记事件A:从上面4件甲班组生产的产品中随机抽取2件,且都是合格品;事件B:从上面5件乙班组生产的产品中随机抽取2件,一件是合格品,一件是次品,试估计这两个事件哪一种情况发生的可能性大.
附:![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(1)甲:![]() ,乙:
,乙:![]() ;(2)没有95%的把握认为此种产品的产品质量与生产产品的班组有关;(3)事件A发生的可能性大一些
;(2)没有95%的把握认为此种产品的产品质量与生产产品的班组有关;(3)事件A发生的可能性大一些
【解析】
(1)直接计算甲班组和乙班组产品的不合格率;(2)利用独立性检验求得没有95%的把握认为此种产品的产品质量与生产产品的班组有关;(3)利用古典概型的概率公式求出P(A)和P(B),再比较大小即得解.
(1)根据表中数据,甲班组生产该产品的不合格率为![]() ,
,
乙班组生产该产品的不合格率为![]() ;
;
(2)列联表如下:
甲班组 | 乙班组 | 合计 | |
合格品 | 75 | 80 | 155 |
次品 | 25 | 20 | 45 |
合计 | 100 | 100 | 200 |
![]() .
.
所以,没有95%的把握认为此种产品的产品质量与生产产品的班组有关.
(3)由题意,若按合格与不合格的比例,则抽取了4件甲班组产品,5件乙班组产品,其中甲、乙班组抽取的产品中均含有1件次品,设这4件甲班组产品分别为A1,A2,A3,D,其中A1,A2,A3代表合格品,D代表次品,从中随机抽取2件,则所有可能的情况为A1A2,A1A3,A1D,A2A3,A2D,A3D共6种,A事件包含3种,故![]() ;设这5件乙班组产品分别为B1,B2,B3,B4,E,其中B1,B2,B3,B4代表合格品,E代表次品,从中随机抽取2件,则所有可能的情况为B1B2,B1B3,B1B4,B1E,B2B3,B2B4,B2E,B3B4,B3E,B4E共10种,B事件包含4种,故
;设这5件乙班组产品分别为B1,B2,B3,B4,E,其中B1,B2,B3,B4代表合格品,E代表次品,从中随机抽取2件,则所有可能的情况为B1B2,B1B3,B1B4,B1E,B2B3,B2B4,B2E,B3B4,B3E,B4E共10种,B事件包含4种,故![]() ;
;
因为P(A)>P(B),所以,事件A发生的可能性大一些.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】汽车在行驶中,由于惯性,刹车后还要继续向前滑行一段距离才能停止,一般称这段距离为“刹车距离”.刹车距离是分析交通事故的一个重要依据.在一个限速为![]() 的弯道上,甲、乙两辆汽车相向而行,突然发现有危险情况,同时紧急刹车,但还是发生了交通事故.事后现场勘查,测得甲车的刹车距离略超过
的弯道上,甲、乙两辆汽车相向而行,突然发现有危险情况,同时紧急刹车,但还是发生了交通事故.事后现场勘查,测得甲车的刹车距离略超过![]() ,乙车的刹车距离略超过
,乙车的刹车距离略超过![]() .已知甲、乙两种车型的刹车距离
.已知甲、乙两种车型的刹车距离![]() 与车速
与车速![]() 之间的关系分别为:
之间的关系分别为:![]() ,
,![]() .根据以上信息判断:在这起交通事故中,应负主要责任的可能是_______________车,理由是__________________________.
.根据以上信息判断:在这起交通事故中,应负主要责任的可能是_______________车,理由是__________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,点
,点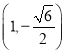 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)圆![]() 是以椭圆
是以椭圆![]() 的焦距为直径的圆,点
的焦距为直径的圆,点![]() 是椭圆
是椭圆![]() 的右顶点,过点
的右顶点,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,若
,若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,
,![]() ,若原点
,若原点![]() 在以
在以![]() 为直径的圆外,求
为直径的圆外,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com