
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
科目:高中数学 来源: 题型:
【题目】某公司近年来科研费用支出![]() 万元与公司所获利润
万元与公司所获利润![]() 万元之间有如表的统计
万元之间有如表的统计
![]()
数据:参考公式:用最小二乘法求出![]() 关于
关于![]() 的线性回归方程为:
的线性回归方程为: ![]() ,
,
其中:  ,
, ![]() ,参考数值:
,参考数值: ![]() 。
。
(Ⅰ)求出![]() ;
;
(Ⅱ)根据上表提供的数据可知公司所获利润![]() 万元与科研费用支出
万元与科研费用支出![]() 万元线性相关,请用最小二乘法求出
万元线性相关,请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)试根据(Ⅱ)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台风中心在港口南偏东![]() 方向上,距离港口
方向上,距离港口![]() 千米处的海面上形成,并以每小时
千米处的海面上形成,并以每小时![]() 千米的速度向正北方向移动,距台风中心
千米的速度向正北方向移动,距台风中心![]() 千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 为
为![]() 上任意两点,且
上任意两点,且![]() 的长为定值,则下面的四个值中不为定值的是( )
的长为定值,则下面的四个值中不为定值的是( )
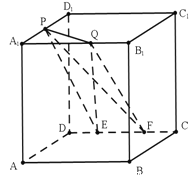
A. 点![]() 到平面
到平面![]() 的距离B. 三棱锥
的距离B. 三棱锥![]() 的体积
的体积
C. 直线![]() 与平面
与平面![]() 所成的角D. 二面角
所成的角D. 二面角![]() 的大小
的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚![]()
秒. A地测得该仪器弹至最高点H时的仰角为30°.
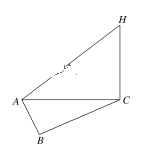
(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com