
【题目】在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为
米到水底进行考古作业.其用氧量包含一下三个方面:①下潜平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升;②水底作业时间范围是最少
升;②水底作业时间范围是最少![]() 分钟最多
分钟最多![]() 分钟,每分钟用氧量为
分钟,每分钟用氧量为![]() 升;③返回水面时,平均速度为
升;③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为
米/分钟,每分钟用氧量为![]() 升.潜水员在此次考古活动中的总用氧量为
升.潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为
,水底作业时间为![]() 分钟,求总用氧量
分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气![]() 升,请问潜水员最多在水下多少分钟(结果取整数)?
升,请问潜水员最多在水下多少分钟(结果取整数)?
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中
其中![]() 为常数.
为常数.
(1)当函数![]() 的图象在点
的图象在点![]() 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数![]() 在
在![]() 上的最小值; (2)若函数
上的最小值; (2)若函数![]() 在区间
在区间![]() 上既有极大值又有极小值,求
上既有极大值又有极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的一种产品的广告费用![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
(1)根据上述数据,求出销售额![]() (万元)关于广告费用
(万元)关于广告费用![]() (万元)的线性回归方程;
(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于![]() 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?
(参考数值: ![]() .
.
回归直线的斜率和截距的最小二乘法估计公式分别为: 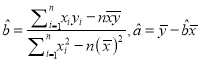 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,则下面结论正确的是 ( )
,则下面结论正确的是 ( )
A. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍, 纵坐标不变,再把得到的曲线向左平移
倍, 纵坐标不变,再把得到的曲线向左平移![]() 个单位长度, 得到曲线
个单位长度, 得到曲线![]()
B. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把![]() 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的![]() 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com