
【题目】已知函数![]() (
(![]() )在
)在![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)设![]() ,
, ![]() ,证明:
,证明: 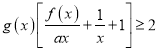 .
.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点. 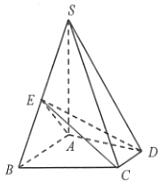
(1)求证:CE∥平面SAD;
(2)求二面角D﹣EC﹣B的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 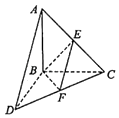
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠城某影院共有100个座位,票价不分等次.根据该影院的经营经验,当每张标价不超过10元时,票可全部售出;当每张票价高于10元时,每提高1元,将有3张票不能售出.为了获得更好的收益,需给影院定一个合适的票价,符合的基本条件是: ①为方便找零和算帐,票价定为1元的整数倍;
②影院放映一场电影的成本费用支出为575元,票房收入必须高于成本支出.
用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入).
(Ⅰ)把y表示成x的函数,并求其定义域;
(Ⅱ)试问在符合基本条件的前提下,每张票价定为多少元时,放映一场的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD;
(Ⅲ)求二面角A﹣PD﹣B的大小.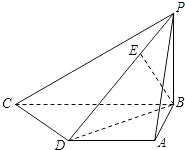
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】持续高温使漳州市多地出现气象干旱,城市用水紧张,为了宣传节约用水,某人准备在一片扇形区域(如图3)上按照图4的方式放置一块矩形ABCD区域宣传节约用水,其中顶点B,C在半径ON上,顶点A在半径OM上,顶点D在 ![]() 上,∠MON=
上,∠MON= ![]() ,ON=OM=10,m,设∠DON=θ,矩形ABCD的面积为S.
,ON=OM=10,m,设∠DON=θ,矩形ABCD的面积为S. 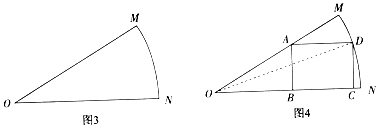
(Ⅰ)用含θ的式子表示DC,OB的长‘
(Ⅱ)若此人布置1m2的宣传区域需要花费40元,试将S表示为θ的函数,并求布置此矩形宣传栏最多要花费多少元钱?(精确到0.01)
(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com